Word break is to divide a string into sub-strings that defined in dictionary. The problem is usually solved with recursion. The time complexity is exponential. Here we introduce word break using memoization, which helps to improve complexity.
Memoization is one of Dynamic programming(DP) techniques. DP is able to solve a complex problem by breaking it down into sub-problems. Each following steps can re-use the result from the previous steps, and avoid redundant calculations or operations. This improves the time complexity significantly, from exponential to O(n^3) or O(n^2).
Declare a variable (called memo) in dfs wrapper method. Its data structure is list or set. Add this variable as one input parameter of dfs helper (recursive) method. At the beginning of the helper method, check whether the input is stored in memo. if it is, return memo value directly. Within the body of helper method, update the memo value before call itself.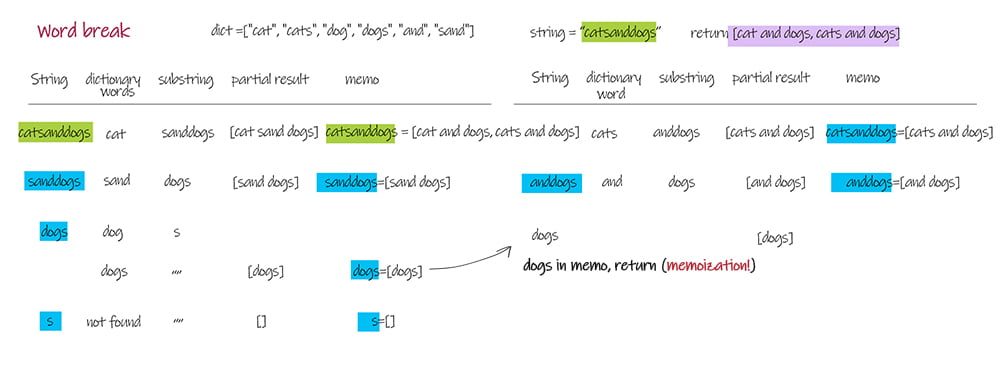
Amazon Interview Question:
How would you like to efficiently find the total number of possible ways with which given string may be converted to whole dictionary words.
Example :
String = “Dogeatscare”
possible combinations – “Dog, eat, scare ” and “Dog, eats, care”
output is 2.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | import java.util.*; public class WordBreak { //Wrapper, Time O(s^3), Space O(s^2) public static int wordBreak(String str, List<String> dict) { List<String> list = helper(str.toLowerCase(), dict, new HashMap<String, List<String>>()); System.out.println(list); return list.size(); } //DFS + memoization, Time worst O(2^s) average O(s^2*w) ~ O(s^3) //when memoziation takes places, extra loop to copy output //Space O(s^2), s is input string length, w is max length of words in dictionary private static List<String> helper(String s, List<String> dict, Map<String, List<String>> memo) { if (memo.containsKey(s)) //use memoization to limit overlap process return memo.get(s); List<String> res = new ArrayList<String>(); for (String w : dict) { if (s.startsWith(w)) { String next = s.substring(w.length()); if (next.length() == 0) res.add(w); else { for (String sub : helper(next, dict, memo)) res.add(w + " " + sub); } } } memo.put(s, res); //save partial results return res; } public static void main(String[] args) { List<String> words = Arrays.asList( "cat", "cats","dog", "dogs", "and", "sand", "scare", "eats", "eat", "care"); //Test case 1 String s = "dogeatscare"; System.out.println("Input: " + s); System.out.println("Word break count: " + wordBreak(s, words)); System.out.println(); //Test case 2 String s1 = "catsanddogs"; System.out.println("Input: " + s1); System.out.println("Word break count: " + wordBreak(s1, words)); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | class WordBreak{ //Wrapper function, Time O(s^3), Space O(s^2) wordBreak (str, dict) { var memo = new Map(); var list = this.helper(str, dict, memo); console.log(list); return list.length; } //DFS + memoization, Time O(s^3), Space O(s^2), //s is input string length, w is max length of words in dictionary helper(s, dict, memo){ if (memo.has(s)) //use memoization to limit overlap process return memo.get(s); var res = new Array(); for (const word of dict) { if(s.startsWith(word)) { let next = s.substring(word.length); if(next.length == 0) res.push(word); else { for(const sub of this.helper(next, dict, memo)) res.push(word + " " + sub); } } } memo.set(s, res); //save partial results return res; } } let wb = new WordBreak(); const dict = ["cat", "cats", "dog", "dogs", "and", "sand"]; let s = "catsanddogs"; console.log(wb.wordBreak(s, dict)); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | class WordBreak: #Wrapper function, Time O(s^3), Space O(s^2) def wordBreak (self, str, dict): memo = {} list = self.helper(str, dict, memo) print(list) return len(list) #DFS + memoization, Time O(s^3), Space O(s^2), #s is input string length, w is max length of words in dictionary def helper(self, s, dict, memo): if s in memo.keys(): #use memoization to limit overlap process return memo.get(s) res = [] for word in dict : if s.startswith(word): next = s[len(word):] if len(next) == 0: res.append(word) else : for sub in self.helper(next, dict, memo): res.append(word + " " + sub) memo[s]=res #save partial results return res wb = WordBreak() dict = ["cat", "cats", "dog", "dogs", "and", "sand"]; s = "catsanddogs"; print(wb.wordBreak(s, dict)); |
Doodle
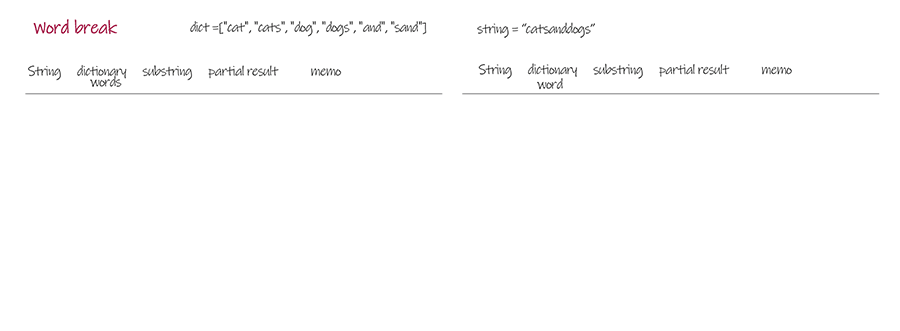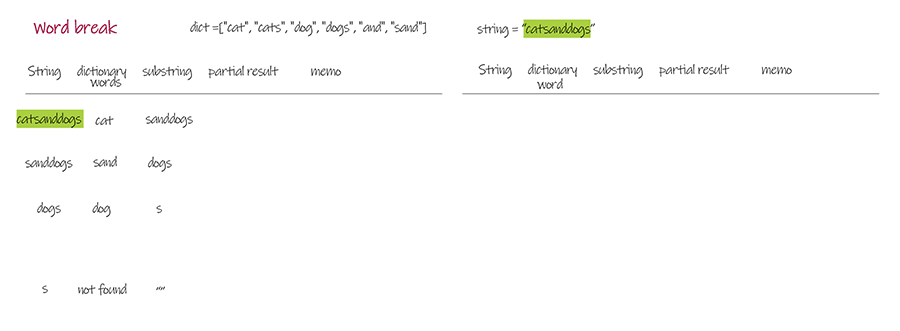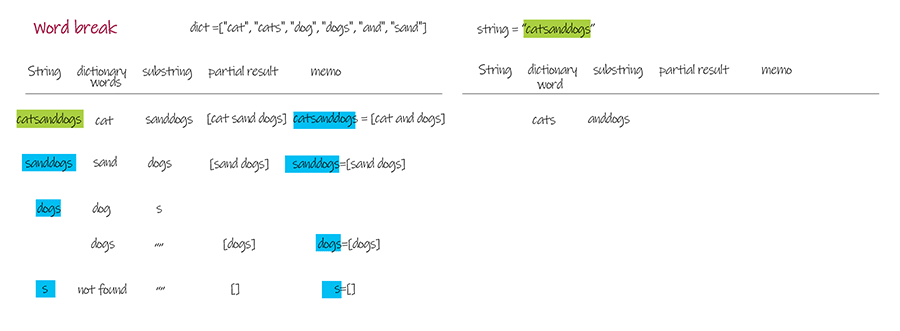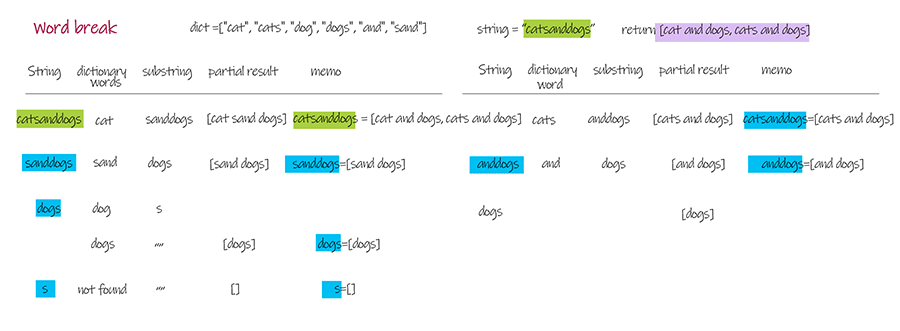
Output:
Input: dogeatscare
[dog eats care, dog eat scare]
Word break count: 2
Input: catsanddogs
[cat sand dogs, cats and dogs]
Word break count: 2
O Notation:
Recursion with memoization:
Time complexity: O(s^3)
Space complexity: O(s^2)
Download WordBreak.java
Download WordBreak.js
Download WordBreak.py
Java Coding Interview Pocket Book





