The modulo operation returns the remainder of one number divided by another. Modulo operator is a arithmetical operator, represented as %. One modulo operation example in math, 6 % 4 is 2.
The modulo operation is also used in circular array. When an array index modulo (or mod) the array length, the index that is larger than length will wrap around to the beginning of the array. Therefore an array becomes a circular array.
% is an operator that are the same cross most programming languages such as Java, JavaScript and Python. Here are two examples of modulo operation in programming. One is in math. The other is used in a circular problem.
1. FizzBuzz
A simple example using modulo operation is Fizzbuzz question.
Question:
Write a program that outputs the string representation of numbers from 1 to n. For a number is multiples of three, it should output “Fizz”. For a number is the multiples of five, outputs “Buzz”. For numbers which are multiples of both three and five, outputs “FizzBuzz”.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | public class FizzBuzz { //Use math mod, Time O(1), Space O(1) public static void fizzBuzz(int n) { if (n % 15 == 0) System.out.println("FizzBuzz"); else if (n % 3 == 0) System.out.println("Fizz"); else if (n % 5 == 0) System.out.println("Buzz"); else System.out.println(String.valueOf(n)); } public static void main(String[] args) { int n = 15; for (int i = 1; i <= n; i++) { fizzBuzz(i); } } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | //Use math mod, Time O(1), Space O(1) function fizzBuzz(num) { if (num % 15 == 0) console.log("FizzBuzz"); else if (num % 3 == 0) console.log("Fizz"); else if (num % 5 == 0) console.log("Buzz"); else console.log(num); } const n = 15; for (let i = 1; i <= n; i++) { fizzBuzz(i); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #Use math mod, Time O(1), Space O(1) def fizzBuzz(num) : if num % 15 == 0: print("FizzBuzz") elif num % 3 == 0 : print("Fizz") elif num % 5 == 0: print("Buzz") else : print(num) n = 15 for i in range(1, n+1): fizzBuzz(i) |
Output:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 1 2 Fizz 4 Buzz Fizz 7 8 Fizz Buzz 11 Fizz 13 14 FizzBuzz |
O Notation:
Time complexity: O(1)
Space complexity: O(1)
2. Round Robin Tournament Scheduler
Here is an example of using modulo operation in circular array – Round Robin Tournament Scheduler. If there are n competitors in tournament. Each competitor meets all others in turn. The details about how it works can be found in wiki. The basis of the algorithm is using circle method. We exclude the first competitor and make all other competitors to form a circle. after each round, the competitors in the circle move forward in 1 spot and compete with different ones.
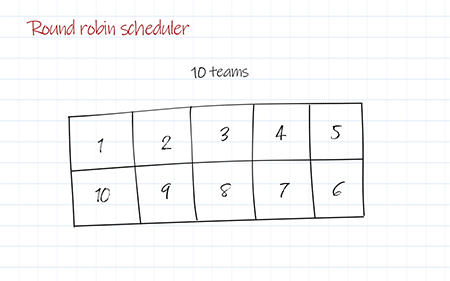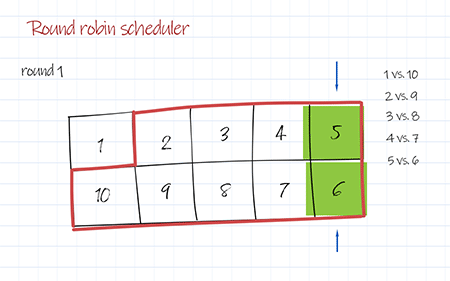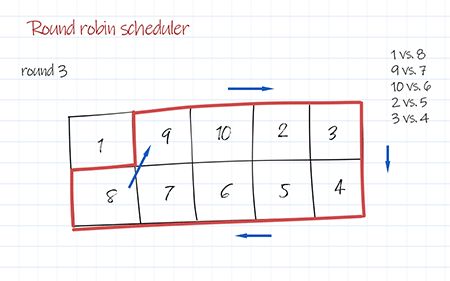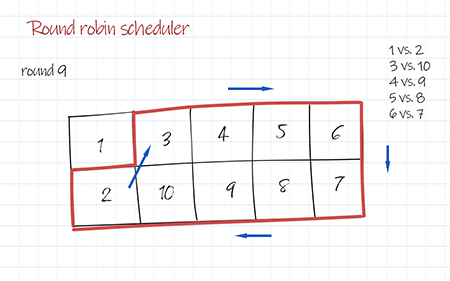
Here we apply modulo operation to implement scheduling algorithm. We put all competitors except the first one in a circular array. The index of two competitor are Nth vs. Nth-from-the-last. For the first competitor, it is index 0 vs. roundNumber%circularSize. Please note, If there are odd number of competitors, a dummy competitor can be added to make total number of teams even. Whoever scheduled to play with “dummy” shall skip in this round.
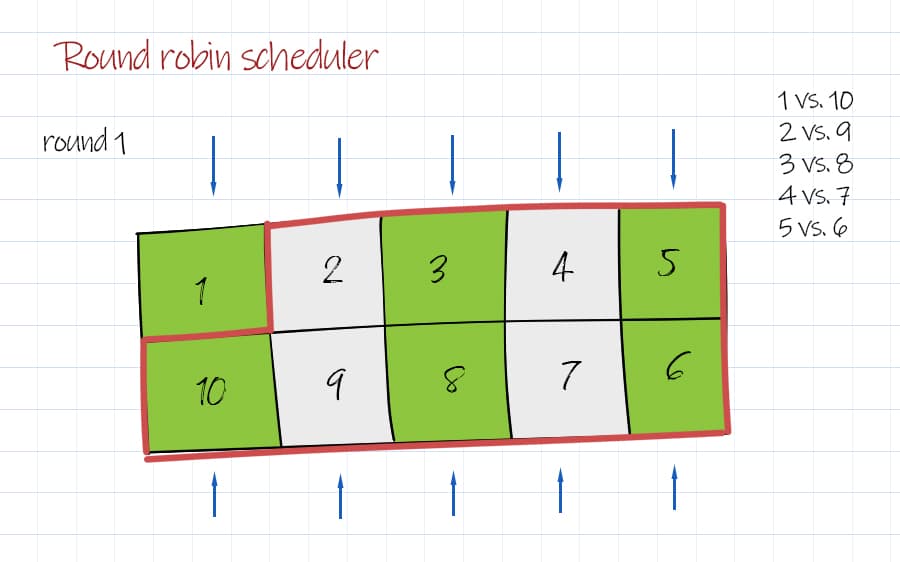
Question:
There are 10 soccer teams that will play in the league. Read the names of the teams and develop a round-robin schedule so that every team plays with every other team over the next 9 weeks.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | public class RoundRobinScheduler { public static void roundRobinScheduler(String[] teams) { int inputTeams = teams.length; String[] newTeams; int k = 0; String dummy ="dummy"; if (inputTeams % 2 == 0) { newTeams = new String[inputTeams-1]; for (k = 0; k < inputTeams-1; k++) //new teams excludes the first team newTeams[k] = teams[k+1]; } else { newTeams = new String[inputTeams]; for(k = 0; k < inputTeams-1; k++) newTeams[k] = teams[k+1]; newTeams[inputTeams-1] = dummy; //if number of input teams is odd number, add a dummy team } int circularSize = newTeams.length ; //teams that's in circle, excluding the first team int allTeams = circularSize + 1; //includes the first team int totalRounds = allTeams - 1; //rounds needed to complete tournament int halfSize = allTeams / 2; //half number of all teams, also number of competing in each round int count = 1; for (int round = totalRounds-1; round >= 0; round--) { System.out.println("round " + (count++)); int teamIdx = round % circularSize; if(!newTeams[teamIdx].equals(dummy)) //first team, that's not in circle System.out.println(teams[0] + " vs. "+ newTeams[teamIdx] ); for (int i = 1; i < halfSize; i++) { //all other teams that are in circle int firstTeam = (round + i) % circularSize; //2nd, 3rd.. int secondTeam = (round + circularSize - i) % circularSize; //2nd to last, 3rd to last.. if ( !newTeams[firstTeam].equals(dummy) && !newTeams[secondTeam].equals(dummy)) //skip dummy System.out.println(newTeams[firstTeam] + " vs. "+ newTeams[secondTeam]); } System.out.println(); } } public static void main(String[] args) { String[] teams = {"1", "2", "3", "4", "5","6", "7", "8", "9","10"}; roundRobinScheduler(teams); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | function roundRobinScheduler(teams) { var inputTeams = teams.length; var newTeams = []; var k = 0; var dummy = "dummy"; if (inputTeams % 2 == 0) { for(k = 0; k < inputTeams-1; k++) //new teams excludes the first team newTeams[k] = teams[k+1]; } else { for(k = 0; k < inputTeams-1; k++) newTeams[k] = teams[k+1]; newTeams[inputTeams-1] = dummy; //if number of input teams is odd number, add a dummy team to make even number } var circularSize = newTeams.length; //teams that's in circle, excluding the first team var allTeams = circularSize +1; //includes the first team var totalRounds = allTeams - 1; // rounds needed to complete tournament var halfSize = allTeams / 2; //half number of all teams, also number of competitions in each round var count = 1; for (let round = totalRounds-1; round >= 0; round--) { console.log("round " + (count++)); let teamIdx = round % circularSize; if (newTeams[teamIdx] !== dummy) //first team, that's not in circle console.log(teams[0] + " vs. "+ newTeams[teamIdx] ); for (let i = 1; i < halfSize; i++) { //all other teams that are in circle let firstTeam = (round + i) % circularSize; //2nd, 3rd.. let secondTeam = (round + circularSize - i) % circularSize; //2nd to last, 3rd to last.. if ( newTeams[firstTeam]!==dummy && newTeams[secondTeam]!== dummy) //skip dummy console.log(newTeams[firstTeam] + " vs. "+ newTeams[secondTeam]); } console.log(); } } const teams = [ "1", "2", "3", "4", "5","6", "7", "8", "9","10"]; roundRobinScheduler(teams) |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | def roundRobinScheduler(teams) : inputTeams = len(teams) k = 0 dummy = "dummy" if (inputTeams % 2 == 0) : newTeams =[None]*(inputTeams-1) for k in range(0, inputTeams-1): #new teams excludes the first team newTeams[k] = teams[k+1] else : newTeams=[None]*inputTeams for k in range (0, inputTeams-1): newTeams[k] = teams[k+1] newTeams[inputTeams-1] = dummy; #if number of input teams is odd number, add a dummy team to make even circularSize = len(newTeams) #teams that's in circle, excluding the first team allTeams = circularSize + 1 #includes the first team totalRounds = allTeams - 1 # rounds needed to complete tournament halfSize = int(allTeams / 2) #half number of all teams, alos number of competitions in each round count = 1 for round in range( totalRounds-1, -1, -1) : print("round " + str(count)) teamIdx = round % circularSize if newTeams[teamIdx] != dummy: #first team, that's not in circle print(teams[0] + " vs. "+ newTeams[teamIdx] ) for i in range( 1, halfSize): #all other teams that are in circle firstTeam = (round + i) % circularSize; #2nd, 3rd.. secondTeam = (round + circularSize - i) % circularSize; #2nd to last, 3rd to last.. if newTeams[firstTeam]!=dummy and newTeams[secondTeam]!= dummy: #skip dummy print(newTeams[firstTeam] + " vs. "+ newTeams[secondTeam]) print() count += 1 teams = [ "1", "2", "3", "4", "5","6", "7", "8", "9","10"] roundRobinScheduler(teams) |
Doodle
Output:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | round 1 1 vs. 10 2 vs. 9 3 vs. 8 4 vs. 7 5 vs. 6 round 2 1 vs. 9 10 vs. 8 2 vs. 7 3 vs. 6 4 vs. 5 round 3 1 vs. 8 9 vs. 7 10 vs. 6 2 vs. 5 3 vs. 4 round 4 1 vs. 7 8 vs. 6 9 vs. 5 10 vs. 4 2 vs. 3 round 5 1 vs. 6 7 vs. 5 8 vs. 4 9 vs. 3 10 vs. 2 round 6 1 vs. 5 6 vs. 4 7 vs. 3 8 vs. 2 9 vs. 10 round 7 1 vs. 4 5 vs. 3 6 vs. 2 7 vs. 10 8 vs. 9 round 8 1 vs. 3 4 vs. 2 5 vs. 10 6 vs. 9 7 vs. 8 round 9 1 vs. 2 3 vs. 10 4 vs. 9 5 vs. 8 6 vs. 7 |
O Notation:
Time complexity: O(n^2)
Space complexity: O(1)
n is number of teams
Download RoundRobinScheduler.java
Download RoundRobinScheduler.js
Download RoundRobinScheduler.py
Round Robin Tournament (GitHub)
The modulo operation returns the remainder of one number divided by another. In Java, it uses % as modulo operator. For example, 6 % 4 = 2.
The modulo operation returns the remainder of one number divided by another. In JavaScript, it uses % as modulo operator. For example, 6 % 4 = 2.
