A flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. A flow network has designated source and sink nodes s and t. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. min cut is one of flow network problem.
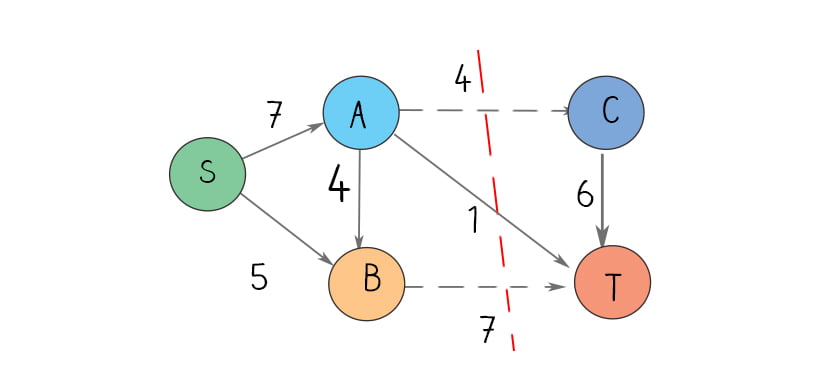
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition. These edges are said to cross the cut. A s-t cut is a cut that requires the source ‘s’ and sink ‘t’ to be in different subsets. The cut-set only consists of edges going from the source’s side to the sink’s side. The capacity of s-t cut is defined by the sum of the capacity of each edge in the cut-set. A minimum s-t cut, or min cut, has the minimum capacity of the cut-set. For example, in the above graph, the min s-t cut-set is {{A, C}{B,T}}.
After you find the minimum s-t cut-set, you classify nodes in a graph as upstream, downstream and central: Upstream nodes: contains all nodes v such that, for all minimum s-t cuts (A, B), v is in A (always on the source side). Downstream nodes: contains all nodes v such that, for all minimum s-t cuts (A, B), v is in B (always on the sink side). Central nodes: contains all nodes v such that there exists some minimum cut where v is on the source side and there exists some minimum cut where v is on the sink side. In the above diagram, the upstream is {A, B, S}, downstream is {C, T}, central is {}.
The min cut is important in flow network analysis because it represents the bottleneck in the network that limits the maximum flow that can be sent from the source to the sink. The max-flow min-cut theorem states that the maximum flow in a flow network is equal to the minimum capacity of any cut in the network. Here you will learn how to implement min cut in flow network.
1. Implement FlowNetwok
A flow network is implemented as a weighted, directed graph. It is represented as a map of maps. In the map G, keys are nodes (of generic type T), and values are map of edges.
In the map of edges, keys are nodes (of generic type T), and values are integers. So, if a node u is a key in the map G, and its map has a key-value pair v, i, then this should be interpreted as the graph having directed edge (u, v) with capacity i. The source and sink parameters are of generic type T; these identify the source and sink nodes of the flow network and can be assumed to be keys in the map G.
Residual Graph of a flow network is a graph which indicates additional possible flow. To make out FlowNetwork class working as residual graph, you have two additional methods fillEmptyEdge(). If an edge has not capacity, set capacity to 0. Another method cloneGraph(), since you update capacity on the way to find the path. After you clone the graph, you make the changes to the cloned graph.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | import java.util.*; public class FlowNetwork<T> { Map<T, Map<T,Integer>> adj = new HashMap<>(); //initialize, add nodes, edges, Time O(1), Space O(1) public void addEdge(T u, T v, int w) { adj.putIfAbsent(u, new HashMap<>()); //add node adj.putIfAbsent(v, new HashMap<>()); //add node Map<T, Integer> edges = adj.get(u); edges.put(v,w); adj.put(u, edges); } //Time O(V2), Space O(V+E) public void fillEmptyEdge(){ for(T t: adj.keySet()) { Map<T, Integer> map=adj.get(t); for (T t1 : adj.keySet()) { if(map.get(t1)==null) { map.put(t1, 0); } } } } //Time O(EV), Space O(E+V) public Map<T, Map<T, Integer>> cloneGraph( Map<T, Map<T, Integer>> g) { Map<T, Map<T, Integer>> clone = new HashMap<>(); for(T t: g.keySet()) { clone.put(t, new HashMap<>()); Map<T, Integer> edges1 = clone.get(t); Map<T, Integer> edges = g.get(t); for (Map.Entry<T, Integer> e: edges.entrySet()) { edges1.put(e.getKey(), e.getValue()); } clone.put(t, edges1); } return clone; } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | class FlowNetwork { constructor() { this.adj = new Map(); } //initialize, add nodes, edges, Time O(1), Space O(1) addEdge(u, v, w) { if (this.adj.get(u) == null) this.adj.set(u, new Map()); //add node if(this.adj.get(v) == null) this.adj.set(v, new Map()); let edge = this.adj.get(u); edge.set(v,w); this.adj.set(u, edge); } //Time O(V2), Space O(V+E) fillEmptyEdge(){ for(let t of this.adj.keys()) { let map=this.adj.get(t); for (let t1 of this.adj.keys()) { if(map.get(t1)==null) { map.set(t1, 0); } } } } //Time O(EV), Space O(E+V) cloneGraph() { let clone = new Map(); for(let t of this.adj.keys()) { clone.set(t, new Map()); let edges1 = clone.get(t); let edges = this.adj.get(t); for (let e of edges.entries()) { edges1.set(e[0], e[1]); } clone.set(t, edges1); } return clone; } } module.exports = FlowNetwork |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | class FlowNetwork : def __init__(self) : self.adj ={} #initialize, add nodes, edges, Time O(1), Space O(1) def addEdge(self, u, v, w): if (self.adj.get(u) is None) : self.adj[u] = {} #add node if(self.adj.get(v) is None): self.adj[v] = {} edge = self.adj.get(u) edge[v] = w self.adj[u] = edge #Time O(V2), Space O(E) def fillEmptyEdge(self) : for t in self.adj.keys() : map= self.adj[t] for t1 in self.adj.keys(): if t1 not in map: map[t1]= 0 #Time O(EV), Space O(E+V) def cloneGraph(self) : clone = {} for t in self.adj.keys(): clone[t] = {} edges1 = clone[t] edges = self.adj[t] for k,v in edges.items(): edges1[k] = v clone[t] = edges1 return clone |
2. Implement cut-partition
Implement an algorithm to produce this partition of nodes. In particular, you should implement a function
static Map cut_partition(<Map> G, T source, T sink)
In the method, clone the graph first. Then by using bfs, you find out if there is a path from source to sink. bfs also builds parent[] array. Using the parent[] array, you traverse through the found path and find possible flow through this path by finding minimum residual capacity along the path. You add the found path flow to overall flow. Meanwhile, you update residual capacities. Subtract path flow from all edges along the path and add path flow along the reverse edges. Meantime you add path flow along reverse edges because you may later need to send flow in reverse direction.
Now use dfs to find all reachable nodes from source and mark it in a Boolean map visited. If reachable, visited value for the node is true, otherwise is false. Now it is time to find the min cut, Check all pairs of nodes, when their edge has capacity, if one’s visited is true and the other’s visited is false, you can add first one to upstream and the second one in downstream.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 | import java.util.*; public class FlowNetworkMinCut<T> { private FlowNetwork<T> flowNetwork; //Time O(1) Space O(1) public FlowNetworkMinCut(FlowNetwork<T> g) { flowNetwork=g; } //Time O(V+E), Space O(V) private boolean bfs(Map<T, Map<T, Integer>> rGraph, T s, T t, Map<T, T> parent) { Map<T, Boolean> visited = new HashMap<>(); for(T x: rGraph.keySet()) visited.put(x,false); Queue<T> q = new LinkedList<>(); q.add(s); visited.put(s,true); parent.put(s,null); while (!q.isEmpty()) { T u = q.poll(); for(T v: rGraph.keySet()) { if (rGraph.get(u).get(v) >0 && !visited.get(v) ){ q.offer(v); parent.put( v,u); visited.put(v, true); } } } return (visited.get(t) == true); } //Time O(V+E), Space O(V) private void dfs(Map<T, Map<T, Integer>> rGraph, T s, Map<T, Boolean> visited) { visited.put(s,true); for(T v: rGraph.keySet()) { if (rGraph.get(s).get(v)>0 && !visited.get(v)) { dfs(rGraph, v, visited); } } } //Time O(V2+E), Space O(V) public void cut_partition(Map<T, Map<T, Integer>> g, T s, T t) { T u,v; Map<T, Map<T, Integer>> rGraph =flowNetwork.cloneGraph(g); Map<T, T> parent = new HashMap<>(); for(T x: rGraph.keySet()) { parent.put(x, null); } //use bfs to find path and update capacity while (bfs(rGraph, s, t, parent)) { int pathFlow = Integer.MAX_VALUE; for (v=t; v!=s; v=parent.get(v)) { u = parent.get(v); pathFlow = Math.min(pathFlow, rGraph.get(u).get(v)); } for (v=t; v!=s; v=parent.get(v)) { u = parent.get(v); //u-v int org = rGraph.get(u).get(v); int update = org-pathFlow; rGraph.get(u).put(v, update); //reverse v-u org = rGraph.get(v).get(u); update = org+pathFlow; rGraph.get(v).put(u, update); } } //use dfs to find the vertices reachable from source Map<T, Boolean> visited = new HashMap<>(); for(T x: rGraph.keySet()) visited.put(x,false); dfs(rGraph, s, visited); //define result Set<T> upStream=new HashSet<>(); Set<T> downStream = new HashSet<>(); Set<T> central = new HashSet<>(); upStream.add(s); downStream.add(t); for(T x: rGraph.keySet()) { if(x!=s && x!=t) central.add(x); } //find min s-t cut-set for(T i: rGraph.keySet()) { for(T j: rGraph.keySet()) { if (g.get(i).get(j)>0 && visited.get(i) && !visited.get(j)) { System.out.println(i + " - " + j); upStream.add(i); downStream.add(j); central.remove(i); central.remove(j); } } } System.out.println("upstream: "+ upStream); System.out.println("downstream: "+downStream); System.out.println("central: "+central); } public static void main(String args[]) { //case1 integer FlowNetwork<Integer> g=new FlowNetwork<>(); g.addEdge(0, 1, 16); g.addEdge(0, 2, 13); g.addEdge(1, 2, 10); g.addEdge(2, 1, 4); g.addEdge(1, 3, 12); g.addEdge(3, 2, 9); g.addEdge(2, 4, 14); g.addEdge(4, 3, 7); g.addEdge(3, 5, 20); g.addEdge(4, 5, 4); g.fillEmptyEdge(); FlowNetworkMinCut<Integer> m = new FlowNetworkMinCut<>(g); m.cut_partition(g.adj, 0, 5); System.out.println(); //test case2, string FlowNetwork<String> g1=new FlowNetwork<>(); g1.addEdge("S", "A", 7); g1.addEdge("S", "B", 5); g1.addEdge("A", "C", 4); g1.addEdge("A", "B", 4); g1.addEdge("C", "T", 6); g1.addEdge("B", "T", 7); g1.fillEmptyEdge(); FlowNetworkMinCut<String> m1 = new FlowNetworkMinCut<>(g1); m1.cut_partition(g1.adj, "S", "T"); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 | const FlowNetwork = require('./FlowNetwork.js') class FlowNetworkMiniCut{ //Time O(V+E), Space O(V) bfs( rGraph, s, t, parent) { var visited = new Map(); for(let x of rGraph.keys()) visited.set(x,false); var q = []; q.push(s); visited.set(s,true); parent.set(s,null); while (q.length>0) { var u = q.shift(); for(let v of rGraph.keys()) { if (rGraph.get(u).get(v) >0 && !visited.get(v) ){ q.push(v); parent.set( v,u); visited.set(v, true); } } } return (visited.get(t) == true); } //Time O(V+E), Space O(V) dfs( rGraph, s, visited) { visited.set(s,true); for(let v of rGraph.keys()) { if (rGraph.get(s).get(v)>0 && !visited.get(v)) { this.dfs(rGraph, v, visited); } } } //Time O(V2+E), Space O(V) cut_partition(g, rGraph, s, t) { var parent = new Map(); for(let x of rGraph.keys()) { parent.set(x, null); } //use bfs to find path and update capacity while (this.bfs(rGraph, s, t, parent)) { var pathFlow = Infinity; for (let v=t; v!=s; v=parent.get(v)) { let u = parent.get(v); pathFlow = Math.min(pathFlow, rGraph.get(u).get(v)); } for (let v=t; v!=s; v=parent.get(v)) { let u = parent.get(v); //u-v let org = rGraph.get(u).get(v); let update = org-pathFlow; rGraph.get(u).set(v, update); //reverse v-u org = rGraph.get(v).get(u); update = org+pathFlow; rGraph.get(v).set(u, update); } } //use dfs to find the vertices reachable from source var visited = new Map(); for(let x of rGraph.keys()) visited.set(x,false); this.dfs(rGraph, s, visited); //define result var upStream=new Set(); var downStream = new Set(); var central = new Set(); upStream.add(s); downStream.add(t); for(let x of rGraph.keys()) { if(x!=s && x!=t) central.add(x); } //find min s-t cut-set for(let i of rGraph.keys()) { for(let j of rGraph.keys()) { if (g.get(i).get(j)>0 && visited.get(i) && !visited.get(j)) { console.log(i + " - " + j); upStream.add(i); downStream.add(j); central.delete(i); central.delete(j); } } } console.log("upstream: "+ Array.from(upStream)); console.log("downstream: "+Array.from(downStream)); console.log("central: "+ Array.from(central)); } } var g= new FlowNetwork(); g.addEdge(0, 1, 16); g.addEdge(0, 2, 13); g.addEdge(1, 2, 10); g.addEdge(2, 1, 4); g.addEdge(1, 3, 12); g.addEdge(3, 2, 9); g.addEdge(2, 4, 14); g.addEdge(4, 3, 7); g.addEdge(3, 5, 20); g.addEdge(4, 5, 4); g.fillEmptyEdge(); var m = new FlowNetworkMiniCut(); var rGraph = g.cloneGraph(); m.cut_partition(g.adj, rGraph, 0, 5); //test case2, string var g1=new FlowNetwork(); g1.addEdge("S", "A", 7); g1.addEdge("S", "B", 5); g1.addEdge("A", "C", 4); g1.addEdge("A", "B", 4); g1.addEdge("C", "T", 6); g1.addEdge("B", "T", 7); g1.fillEmptyEdge(); var m1 = new FlowNetworkMiniCut(); var rGraph1 = g1.cloneGraph(); m1.cut_partition(g1.adj, rGraph1, "S", "T"); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 | import FlowNetwork class MiniCut: #Time O(1), Space O(1) def __init__(self, graph): self.graph = graph #Time O(V+E), Space O(V) def bfs(self, rGraph, s, t, parent): visited ={} for x in rGraph.keys(): visited[x] = False queue=[] parent[s] = None; queue.append(s) visited[s] = True while queue: u = queue.pop(0) for v in rGraph.keys(): if visited[v] == False and rGraph[u][v] > 0 : queue.append(v) parent[v] = u visited[v] = True return True if visited[t] else False #Time O(V+E), Space O(V) def dfs(self, rgraph,s,visited): visited[s]=True for v in rgraph.keys(): if rgraph[s][v]>0 and visited[v] == False: self.dfs(rgraph,v,visited) #Time O(V2+E), Space O(V) def cut_partition(self, g, source, sink): parent = {} rGraph = self.graph.cloneGraph() for x in rGraph.keys(): parent[x] = None #use bfs to find path and update capacity while self.bfs(rGraph, source, sink, parent) : path_flow = float("Inf") v = sink while(v != source): u= parent[v] path_flow = min (path_flow, rGraph[u][v]) v= parent[v] v = sink while(v != source): u = parent[v] rGraph[u][v] -= path_flow rGraph[v][u] += path_flow v = parent[v] #use dfs to find the vertices reachable from source visited ={} for x in rGraph.keys(): visited[x]=False self.dfs(rGraph, source, visited) # define result upStream=set() downStream = set() central = set() upStream.add(source) downStream.add(sink) for x in rGraph.keys(): if x!=source and x!=sink: central.add(x) #find min s-t cut-set for i in rGraph.keys(): for j in rGraph.keys() : if g[i][j]>0 and visited[i] and visited[j] == False : print (str(i) + " - " + str(j)) upStream.add(i) downStream.add(j) if i in central: central.remove(i) if j in central: central.remove(j) print("upstream: "+ str(upStream)) print("downstream: "+str(downStream)) print("central: "+ str(central)) g= FlowNetwork.FlowNetwork() g.addEdge(0, 1, 16) g.addEdge(0, 2, 13) g.addEdge(1, 2, 10) g.addEdge(2, 1, 4) g.addEdge(1, 3, 12) g.addEdge(3, 2, 9) g.addEdge(2, 4, 14) g.addEdge(4, 3, 7) g.addEdge(3, 5, 20) g.addEdge(4, 5, 4) g.fillEmptyEdge() m = MiniCut(g); m.cut_partition(g.adj, 0, 5) print() g1= FlowNetwork.FlowNetwork() g1.addEdge("S", "A", 7); g1.addEdge("S", "B", 5); g1.addEdge("A", "C", 4); g1.addEdge("A", "B", 4); g1.addEdge("C", "T", 6); g1.addEdge("B", "T", 7); g1.fillEmptyEdge(); m1 = MiniCut(g1); m1.cut_partition(g1.adj, "S", "T") print() |
Output:
upstream: [0, 1, 4]downstream: [3, 5]
central: [2]
upstream: [A, B, S]
downstream: [C, T]
central: []
O Notation:
Time complexity: O(V2+E)
Space complexity: O(V)
V is number of nodes, E is number of edges
Download
Download FlowNetworkMinCutJava.zip
Download FlowNetworkMinCutJavaScript.zip
Download FlowNetworkMinCutPython.zip





