To sort squares of a sorted array, you don’t want to use any sorting algorithms such as bubble sort. Because it takes O(nlogn) ~ O(n^2) time. Here we introduce a better way to sort in one pass.
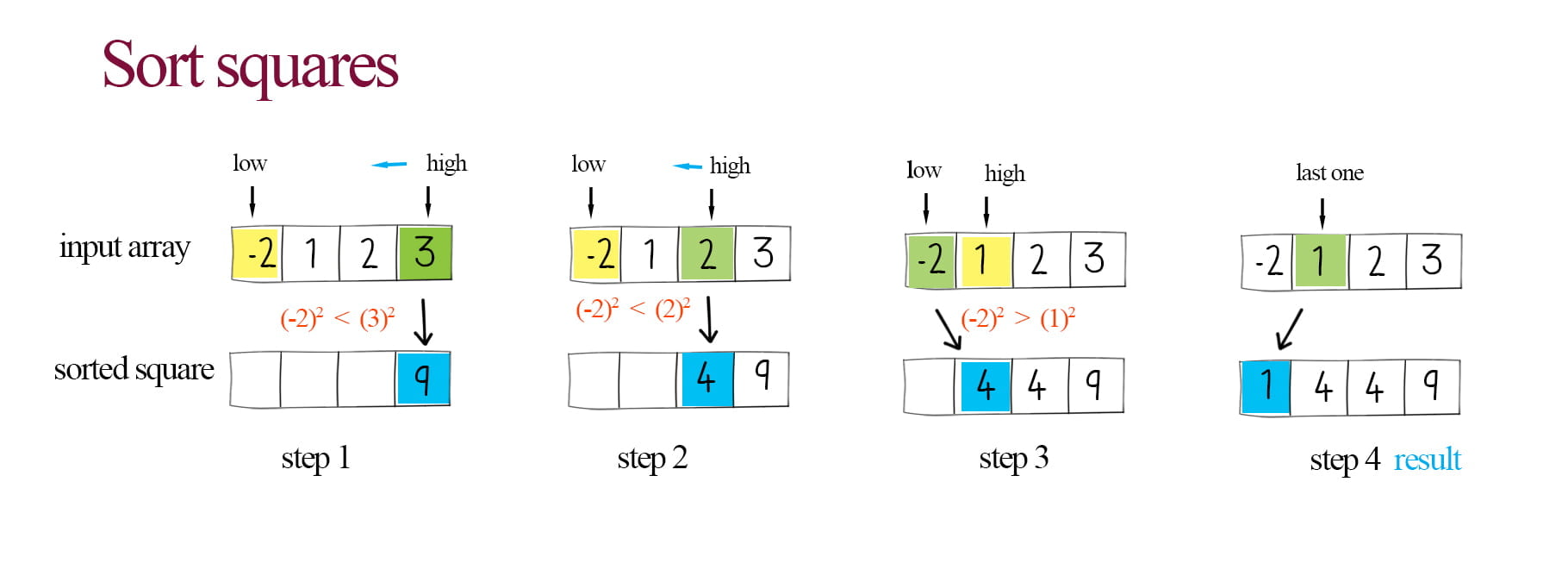
The solution is using two pointers. Initialize two pointers, one points to the first element, and the other points to the last element. Then compare the absolute value of these two elements pointed by the indices. Put the square of the larger one at the end of the output array. Then increase or decrease the larger one’s index. When all the elements have been compared, the output is the sorted square. With the optimized version of sort squares of a sorted array, the solution has the time complexity to O(n).
Question statement:
Input: sorted integers: example: [-2, 1, 2, 3]
Output: sorted squares of the input: [1, 4, 4 ,9]
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | import java.util.Arrays; public class SortSquares { //Two pointers, Time O(n), Space O(n), n is array length public static int[] sortSquares(int[] a) { int n = a.length; int[] res = new int[n]; int i = 0, j = n - 1; for (int k = n-1; k >= 0; k--) { if (Math.abs(a[i]) > Math.abs(a[j])) { res[k] = a[i] * a[i]; i++; } else { res[k] = a[j] * a[j]; j--; } } return res; } public static void main(String[] args) { int[] a = {-2, 1, 2, 3}; System.out.print("Input: "); System.out.println(Arrays.toString(a)); int[] b = sortSquares(a); System.out.print("Sort squares: "); System.out.println(Arrays.toString(b)); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Two pointers, Time O(n), Space O(n), n is array length function sortSquares(a) { var n = a.length; var res = []; var i = 0, j = n - 1; for (let k = n-1; k >= 0; k--) { if (Math.abs(a[i]) > Math.abs(a[j])) { res[k] = a[i] * a[i]; i++; } else { res[k] = a[j] * a[j]; j--; } } return res; } let a = [-2, 1, 2, 3] let b = sortSquares(a) console.log(b) |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #Two pointers, Time O(n), Space O(n), n is array length def sortSquares(a) : n = len(a) res = [None]* n i = 0 j = n - 1 for k in range (n-1, -1, -1) : if abs(a[i]) > abs(a[j]): res[k] = a[i] * a[i] i+=1 else : res[k] = a[j] * a[j] j-=1 return res a = [-2, 1, 2, 3] b = sortSquares(a) print(b) |
Output:
Input array: [-2, 1, 2, 3]
Sorted squares: [1, 4, 4, 9]
O Notation:
Time complexity: O(n)
Space complexity: O(n)
Given a sorted array, return the squares of each element in the array and the squares are sorted. You don’t need sorting algorithm. Instead you use two pointers, one points to the first element, and the other points to the last element. Then compare the squares of these two elements pointed by the indices. Put the square of the larger one at the end of the output array.
Download SortSquares.java
Download SortSquares.js
Download SortSquares.py





