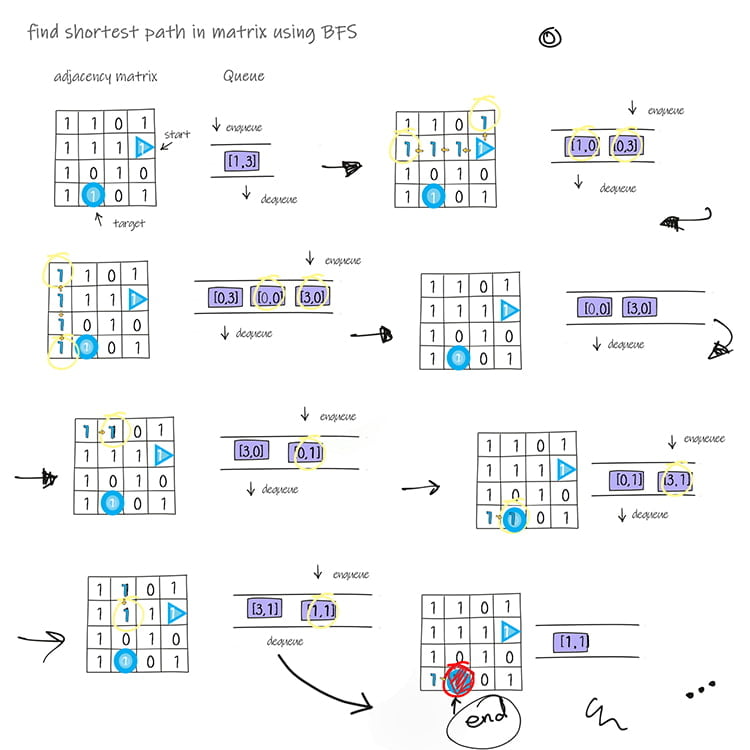
Shortest path in matrix is to find the shortest distance from the the source to the destination. As you know, graph can be represented as adjacent matrix. Therefore, we can use the Breadth First Search algorithm in graph to solve this problem.
BFS starts from the source node. It explores all its adjacent nodes before going to the next level adjacent nodes. It is usually implemented with Queue. You visit each node in the queue until you find the destination. This question allows you to move in 4 directions, i.e, left, right, up and down. So, when visiting each node in queue, your next move is to visit cell’s 4 neighbors.
The trick about this question is that you are no only required to return shortest distance. You are also required to print the shortest path. The solution is to save the previous visited nodes in the cell object. At the end, you use linked list to track all nodes from destination to the source.
Facebook Interview Question:
Given a MxN matrix where each element can either be 0 or 1. We need to print the shortest path between a given source cell to a destination cell. The path can only be created out of a cell if its value is 1.
public void print(int[][] matrix, int[] start, int[] end){
}
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 | import java.util.LinkedList; public class ShortestPathBetweenCellsBFS { private static class Cell { int x; int y; int dist; //distance Cell prev; //parent cell in the path Cell(int x, int y, int dist, Cell prev) { this.x = x; this.y = y; this.dist = dist; this.prev = prev; } @Override public String toString(){ return "(" + x + "," + y + ")"; } } //BFS, Time O(n^2), Space O(n^2) public static void shortestPath(int[][] matrix, int[] start, int[] end) { int sx = start[0], sy = start[1]; int dx = end[0], dy = end[1]; //if start or end value is 0, return if (matrix[sx][sy] == 0 || matrix[dx][dy] == 0) { System.out.println("There is no path."); return; } //initialize the cells int m = matrix.length; int n = matrix[0].length; Cell[][] cells = new Cell[m][n]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (matrix[i][j] != 0) { cells[i][j] = new Cell(i, j, Integer.MAX_VALUE, null); } } } //breadth first search LinkedList<Cell> queue = new LinkedList<>(); Cell src = cells[sx][sy]; src.dist = 0; queue.add(src); Cell dest = null; Cell p; while ((p = queue.poll()) != null) { //find destination if (p.x == dx && p.y == dy) { dest = p; break; } // moving up visit(cells, queue, p.x - 1, p.y, p); // moving down visit(cells, queue, p.x + 1, p.y, p); // moving left visit(cells, queue, p.x, p.y - 1, p); //moving right visit(cells, queue, p.x, p.y + 1, p); } //compose the path if path exists if (dest == null) { System.out.println("there is no path."); return; } else { LinkedList<Cell> path = new LinkedList<>(); p = dest; do { path.addFirst(p); } while ((p = p.prev) != null); System.out.println(path); } } //function to update cell visiting status, Time O(1), Space O(1) private static void visit(Cell[][] cells, LinkedList<Cell> queue, int x, int y, Cell parent) { //out of boundary if (x < 0 || x >= cells.length || y < 0 || y >= cells[0].length || cells[x][y] == null) { return; } //update distance, and previous node int dist = parent.dist + 1; Cell p = cells[x][y]; if (dist < p.dist) { p.dist = dist; p.prev = parent; queue.add(p); } } public static void main(String[] args) { int[][] matrix = { {1, 0, 1}, {0, 1, 1}, {0, 0, 1}}; //case1, there is no path int[] start = {0, 0}; int[] end = {1, 1}; System.out.print("case 1: "); shortestPath(matrix, start, end); //case 2, there is path int[] start1 = {0, 2}; int[] end1 = {1, 1}; System.out.print("case 2: "); shortestPath(matrix, start1, end1); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 | class Cell { constructor(x, y, dist, prev) { this.x = x; this.y = y; this.dist = dist; //distance this.prev = prev; //parent cell in the path } toString() { return "(" + this.x + ", " + this.y + ")"; } } class ShortestPathBetweenCellsBFS { //BFS, Time O(n^2), Space O(n^2) shortestPath(matrix, start, end) { var sx = start[0]; var sy = start[1]; var dx = end[0]; var dy = end[1]; //if start or end value is 0, return if (matrix[sx][sy] == 0 || matrix[dx][dy] == 0) { console.log("There is no path."); return; } //initialize the cells var m = matrix.length; var n = matrix[0].length; var cells = []; for (let i = 0; i < m; i++) { cells[i] = []; for (let j = 0; j < n; j++) { if (matrix[i][j] != 0) { cells[i][j] = new Cell(i, j, Number.MAX_VALUE, null); } } } //breadth first search var queue = []; var src = cells[sx][sy]; src.dist = 0; queue.push(src); var dest = null; var p; while ((p = queue.shift()) != null) { //find destination if (p.x == dx && p.y == dy) { dest = p; break; } // moving up this.visit(cells, queue, p.x-1, p.y, p); // moving left this.visit(cells, queue, p.x, p.y-1, p); // moving down this.visit(cells, queue, p.x+1, p.y, p); //moving right this.visit(cells, queue, p.x, p.y+1, p); } //compose the path if path exists if (dest == null) { console.log("there is no path."); return; } else { let path = []; p = dest; do { path.unshift(p); } while ((p = p.prev) != null); console.log(`${path}`); } } //function to update cell visiting status, Time O(1), Space O(1) visit(cells, queue, x, y, parent) { //out of boundary if (x < 0 || x >= cells.length || y < 0 || y >= cells[0].length || cells[x][y] == null) { return; } //update distance, and previous node var dist = parent.dist + 1; var p = cells[x][y]; if (dist < p.dist) { p.dist = dist; p.prev = parent; queue.push(p); } } } const matrix = [ [1, 0, 1], [0, 1, 1], [0, 0, 1]]; myObj = new ShortestPathBetweenCellsBFS(); //case1, there is no path let start = [0, 0]; let end = [1, 1]; console.log("case 1: "); myObj.shortestPath(matrix, start, end); //case 2, there is path let start1 = [0, 2]; let end1 = [1, 1]; console.log("case 2: "); myObj.shortestPath(matrix, start1, end1); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 | import sys import queue class Cell : def __init__(self, x, y, dist, prev) : self.x = x self.y = y self.dist = dist; #distance to start self.prev = prev; #parent cell in the path def __str__(self): return "("+ str(self.x) + "," + str(self.y) + ")" class ShortestPathBetweenCellsBFS : #BFS, Time O(n^2), Space O(n^2) def shortestPath(self, matrix, start, end) : sx = start[0] sy = start[1] dx = end[0] dy = end[1] #if start or end value is 0, return if matrix[sx][sy] == 0 or matrix[dx][dy] == 0 : print("There is no path.") return #initialize the cells m = len(matrix) n = len(matrix[0]) cells = [] for i in range (0, m) : row = [] for j in range(0, n) : if matrix[i][j] != 0 : row.append(Cell(i, j, sys.maxsize, None)) else: row.append(None) cells.append(row) #breadth first search queue = [] src = cells[sx][sy] src.dist = 0 queue.append(src) dest = None p = queue.pop(0) while p != None : #find destination if p.x == dx and p.y == dy : dest = p break # moving up self.visit(cells, queue, p.x-1, p.y, p) # moving left self.visit(cells, queue, p.x, p.y-1, p) # moving down self.visit(cells, queue, p.x+1, p.y, p) #moving right self.visit(cells, queue, p.x, p.y+1, p) if len(queue) > 0: p = queue.pop(0) else: p = None #compose the path if path exists if dest == None : print("there is no path.") return else : path = [] p = dest while p != None : path.insert(0, p) p = p.prev for i in path: print(i) #function to update cell visiting status, Time O(1), Space O(1) def visit(self, cells, queue, x, y, parent) : #out of boundary if x < 0 or x >= len(cells) or y < 0 or y >= len(cells[0]) or cells[x][y] == None : return #update distance, and previous node dist = parent.dist + 1 p = cells[x][y] if dist < p.dist : p.dist = dist p.prev = parent queue.append(p) matrix = [ [1, 0, 1], [0, 1, 1], [0, 0, 1]] myObj = ShortestPathBetweenCellsBFS() #case1, there is no path start = [0, 0] end = [1, 1] print("case 1: ") myObj.shortestPath(matrix, start, end) #case 2, there is path start1 = [0, 2] end1 = [1, 1] print("case 2: ") myObj.shortestPath(matrix, start1, end1) |
Output:
case 1: there is no path.
case 2: [(0,2), (1,2), (1,1)]
O Notation:
Time complexity: O(mxn)
Space complexity: O(mxn)
m is number of rows, n is number of columns
Download ShortestPathBetweenCellsBFS.java
Download ShortestPathBetweenCellsBFS.js
Download ShortestPathBetweenCellsBFS.py
Shortest path between cells in matrix (YouTube)
Java Coding Interview Pocket Book (2nd Edition)





