A Euler path (Eulerian path) is a path in a graph that you visit each edge exactly once. You can visit the same vertex multiple times though. Dominoes is one example of finding Euler path problem. A domino is a game piece that has 2 numbers on it, one number on top and another underneath. Given a set of dominoes, order them so that number on bottom of the domino in front is equal to the number on top of the domino behind.
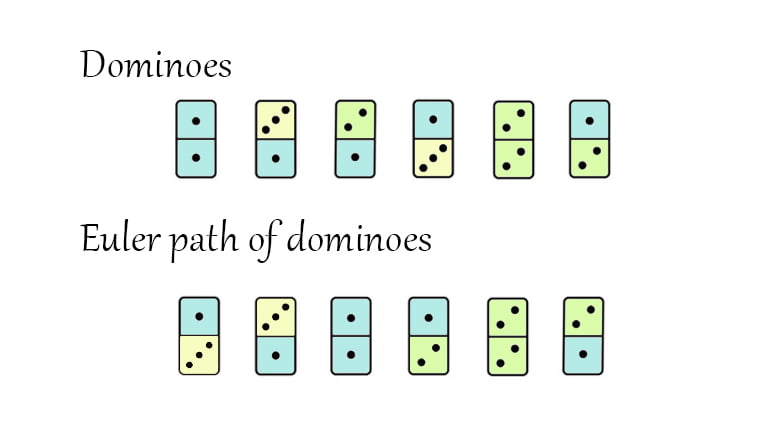
Note dominoes is not an Eulerian circuit in which the start and the end should be the same. Meanwhile, it is undirected. A domino (2,3) is the same as (3,2). It allows duplicated pieces. Traditionally, there are some algorithms to solve Euler path, such as Fleury’s algorithm and Hierholzer’s algorithm. The time complexity is O(E^2) and O(E) respectively. Here we use another method to solve, backtracking.
Actually Hierholzer’s algorithm is using backtracking. When you reach dead end, you return and find another routes. This is the same idea, except here you use recursion. You pick dominoes one by one. Compare itself with the last one. If they match, save it in an output list and remove it from the input set. Then call itself with a smaller set of input. Since the dominoes are undirected, you switch up side down and repeat the same process.
When the recursive function returns, that means this is not a good route. You backtrack by removing the domino piece from the output list and add it back to the input list. On the other hand, if the output list reaches the length of the original input list, that means the function finds a Euler path. You can return from the program. The time complexity is O(E^2).
Using recursive backtracking is a quick brute force solution when you don’t know anything about graph data structure or algorithms in graph. However, it is not efficient. The solution only works fine when the input set is small. Recursive function requires memory space for call stacks. In a case a set is big and there is no Euler path, the recursive function will cause stack overflow.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | import java.util.*; public class FindDominosChain { //backtracking wrapper, Time O(E^2), Space O(E^2), E is number of edges, public static ArrayList<int[]> backtracking(ArrayList<int[]> input) { int inputsize = input.size(); ArrayList<int[]> res = new ArrayList<>(); makeChain(input, res, inputsize); return res; } // recursive method, Time O(E^2), Space O(E^2) private static void makeChain(ArrayList<int[]> input, ArrayList<int[]> res, int inputsize) { for (int i = 0; i < input.size(); i++) { int[] dom = input.get(i); if (res.isEmpty() || res.get(res.size()-1)[1] == dom[0]) { //check whether they can be chained res.add(dom); if (res.size() == inputsize) { //reach the length return; } int[] saved = input.remove(i); makeChain(input, res, inputsize); input.add(i, saved); //backtracking res.remove(res.size()-1); } dom = new int[]{dom[1], dom[0]}; //reverse, both way if (res.isEmpty() || res.get(res.size()-1)[1] == dom[0]) { res.add(dom); if (res.size() == inputsize) { return; } int[] saved = input.remove(i); makeChain(input, res, inputsize); input.add(i, saved); //backtracking res.remove(res.size()-1); } } } //Time O(E) Space O(1) private static void printChain(List<int[]> chain){ for (int i = 0; i<chain.size();i++) System.out.print("["+chain.get(i)[0]+", " + chain.get(i)[1]+"] " ); System.out.println(); } public static void main(String... args) { ArrayList<int[]> input = new ArrayList<>(); input.add(new int[]{1,1}); input.add(new int[]{3,1}); input.add(new int[]{2,1}); input.add(new int[]{1,3}); input.add(new int[]{2,2}); input.add(new int[]{1,2}); System.out.println("input:"); printChain(input); ArrayList<int[]> output = backtracking(input); System.out.println("backtracking:"); printChain(output); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | //backtracking wrapper, Time O(E^2), Space O(E^2), E is number of edges, function backtracking(input) { var inputsize = input.length; var res = []; makeChain(input, res, inputsize); return res; } // recursive method, Time O(E^2), Space O(E^2) function makeChain(input, res, inputsize ) { for (let i = 0; i < input.length; i++) { var dom = input[i]; if (res.length == 0 || res[res.length-1][1] == dom[0]) { //check whether they can be chained res.push(dom); if (res.length == inputsize) { //reach the length return; } let saved = input.splice(i,1); //remove at i makeChain(input, res, inputsize); input.splice(i, 0, saved); //backtracking, insert at index res.splice(res.length-1, 1); //remove last } dom = [dom[1], dom[0]]; //reverse, both way if (res.length == 0 || res[res.length-1][1] == dom[0]) { res.push(dom); if (res.length == inputsize) { return; } var saved = input.splice(i,1 ); //remove at i makeChain(input, res, inputsize); input.splice(i, 0, saved); //backtracking, add at i res.splice(res.length-1, 1); } } } //Time O(E) Space O(1) function printChain(chain){ var line = ""; for (let i = 0; i < chain.length; i++) line+= "["+chain[i][0] +", " + chain[i][1]+"] " ; console.log(line); } var input = []; input.push([1, 1]); input.push([3, 1]); input.push([2, 1]); input.push([1, 3]); input.push([2, 2]); input.push([1, 2]); console.log("input:"); printChain(input); var output = backtracking(input); console.log("Backtracking:"); printChain(output); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | #backtracking wrapper, Time O(E^2), Space O(E^2), E is number of edges, def backtracking(input): inputsize = len(input) res = [] makeChain(input, res, inputsize) return res # recursive method, Time O(E^2), Space O(E^2) def makeChain(input, res, inputsize ) : for i in range(0, len(input)): dom = input[i] if len(res) == 0 or res[len(res)-1][1] == dom[0] : #check whether they can be chained res.append(dom) if (len(res) == inputsize) : # reach the length, stop return; saved = input.pop(i); # remove at i makeChain(input, res, inputsize) input.insert(i, saved) # backtracking, insert at index res.pop(len(res)-1) #remove last dom = [dom[1], dom[0]] #reverse, both way if len(res) == 0 or res[len(res)-1][1] == dom[0] : res.append(dom) if (len(res) == inputsize) : return saved = input.pop(i); #remove at i makeChain(input, res, inputsize) input.insert(i, saved); #backtracking, add at i res.pop(len(res)-1) # print, Time O(E), Space O(1) def printChain(chain) : for i in range(0, len(chain)): print("["+str(chain[i][0]) +", " + str(chain[i][1])+"] ", end=' ' ) print() input = [] input.push([1, 1]); input.push([3, 1]); input.push([2, 1]); input.push([1, 3]); input.push([2, 2]); input.push([1, 2]); print("input:") printChain(input) output = backtracking(input) print("Backtracking:") printChain(output) |
Output:
input:
[1, 1] [3, 1] [2, 1] [1, 3] [2, 2] [1, 2]
Backtracking:
[1, 1] [1, 3] [3, 1] [1, 2] [2, 2] [2, 1]
O Notation:
Time complexity: O(E^2), E is number of dominoes
Space complexity: O(E^2)
Download FindDominosChain.java
Download FindDominosChain.js
Download FindDominosChain.py





