In mathematics expressions, there are infix, prefix and postfix notations. Infix notation is characterized by the placement of operators between operands. For example, the plus sign in 2 + 2. Prefix notation is a notation in which operators precede their operands, such as + 3 4. Postfix notation is a notation in which operators follow their operands, for example 3 4 +. This post introduces how to convert an expression from prefix to postfix. There are two methods, stack and recursion. We use letters as operands in the expression.
The common approach is to use stack to convert prefix to postfix. In this method, we start from the back of expression and scan each character. If the character is a letter, we push the operands in stack. If the character is an operator, such as +,-, * or /, we pop two items from the stack. They are two operands. We concatenate two operands and the operator as one string. It is a postfix sub-expression. Then push the new expression in stack. At the end, the top element in stack is the final postfix expression.
We can also use recursion. In this method, we start from the beginning of the expression. Since in an infix expression, the first character is always operator. The recursive method removes the first character and save it to an variable op. Next the method calls itself twice recursively to get the following two operands, saved as op1 and op2. Then declare a list to store a postfix sub-expression. This expression store op1, op2, and op as elements of list in sequence. When the last recursion returns from call stacks, the list has the final postfix expression.
Google Interview Question:
convert Prefix_to_Postfix using recursion
+ * A B / C D -> A B * C D / +
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | import java.util.*; public class PrefixToPostfix { //Solution 1: Use stack, Time O(n), Space O(m), //n is expression length, m is operator number in expression public static String preToPostStack(char[] exp) { Stack<String> s = new Stack<>(); int length = exp.length; for (int i = length - 1; i >= 0; i--) { if (!isOp(exp[i])) { s.push(Character.toString(exp[i])); } else { String op1 = s.pop(); String op2 = s.pop(); String temp = op1 + op2 + exp[i]; s.push(temp); } } return s.peek(); } //Solution 2: Use recursion, Time O(n), Space O(n+m), public static ArrayList<String> preToPostRec(ArrayList<String> exp) { String op = exp.remove(0); List<String> op1 = isOp(exp.get(0).charAt(0)) ? preToPostRec(exp) : Arrays.asList(exp.remove(0)); List<String> op2 = isOp(exp.get(0).charAt(0)) ? preToPostRec(exp) : Arrays.asList(exp.remove(0)); ArrayList<String> res = new ArrayList<>(exp.size()); res.addAll(op1); res.addAll(op2); res.add(op); return res; } //Check whether the char is operator, Time O(1), Space O(1) private static boolean isOp(char Op) { if (Op == '+' || Op == '-' || Op == '*' || Op == '/') { return true; } else { return false; } } //Utility method, convert list to string, Time O(n), Space O(n), n is list length private static String convert(ArrayList<String> s) { String res = ""; for (String i: s) { res += i; } return res; } public static void main(String[] args) { String s ="+*AB/CD"; //A*B + C/D System.out.println("postfix(stack): " + preToPostStack(s.toCharArray())); ArrayList<String> input = new ArrayList<>(Arrays.asList(s.split(""))); ArrayList<String> output = preToPostRec(input); System.out.println("postfix(recursion): " + convert(output)); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | //Solution 1: Use stack, Time O(n), Space O(m), //n is expression length, m is operator number in expression function preToPostStack(exp) { var s = []; var length = exp.length; for (let i = length - 1; i >= 0; i--) { if (!isOp(exp[i])) { s.push(exp[i]); } else { let op1 = s.pop(); let op2 = s.pop(); let temp = op1 + op2 + exp[i]; s.push(temp); } } return s[s.length - 1]; } //Solution 2: Use recursion, Time O(n), Space O(n+m) function preToPostRec(exp) { var op = exp.shift(0); var op1 = isOp(exp[0].charAt(0)) ? preToPostRec(exp) : exp.shift(); var op2 = isOp(exp[0].charAt(0)) ? preToPostRec(exp) : exp.shift(); var res = new Array(); res.push(op1); res.push(op2); res.push(op); return res; } //Check whether the char is operator, Time O(1), Space O(1) function isOp(op) { if (op == '+' || op == '-' || op == '*' || op == '/') { return true; } else { return false; } } //utility functioin, convert list to string, Time O(n), Space O(n), n is list length function convert(res) { let r = "" for (let i of res) { if (Array.isArray(i)) r += convert(i); else r += i; } return r; } let s ="+*AB/CD"; //A*B + C/D console.log("postfix(stack): " + preToPostStack(s)); let res = preToPostRec(Array.from(s)) r = convert(res); console.log("postfix(rec): " + r); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #Solution 1: Use stack, Time O(n), Space O(m), # n is expression length, m is operator number in expression def preToPostStack(exp) : s = [] length = len(exp) for i in range(length-1, -1, -1) : if isOp(exp[i])==False : s.append(exp[i]) else : op1 = s.pop() op2 = s.pop() temp = op1 + op2 + exp[i] s.append(temp) return s[len(s) - 1] #Solution 2: Use recursion, Time O(n), Space O(n+m) def preToPostRec(exp) : op = exp.pop(0); op1 = preToPostRec(exp) if isOp(exp[0][0]) else exp.pop(0) op2 = preToPostRec(exp) if isOp(exp[0][0]) else exp.pop(0) res = [] res.append(op1) res.append(op2) res.append(op) return res #Check whether the char is operator, Time O(1), Space O(1) def isOp(op): if op == '+' or op == '-' or op == '*' or op == '/' : return True else : return False #Utility function, convert list to string, Time O(n), Space O(n), n is list length def convert(res): r = "" for i in res: if isinstance(i, list): r += convert(i) else: r += i return r s = "+*AB/CD"; #A*B + C/D print("postfix(stack): " + preToPostStack(s)) res = preToPostRec(list(s)) r = convert(res) print("postfix(rec): " + r) |
Doodle
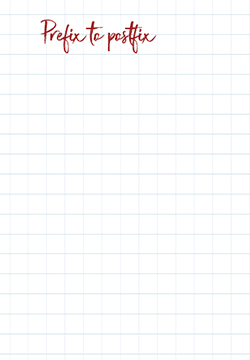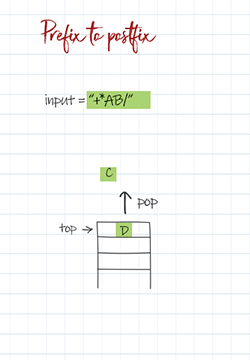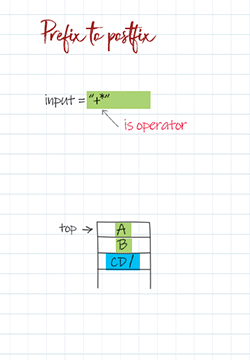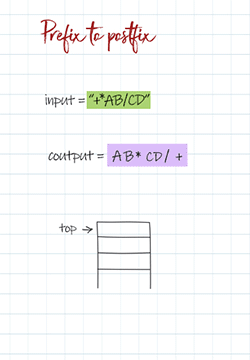
Output:
prefix: +*AB/CD
postfix(stack): AB*CD/+
postfix(recursion): AB*CD/+
O Notation:
Time complexity: O(n)
Space complexity: O(n)
Download PrefixToPostfix.java
Download PrefixToPostfix.js
Download PrefixToPostfix.py
Covert prefix to postfix using stack or recursion (YouTube)
Java Coding Interview Pocket Book
There are two methods. One is using stack. You start from the back of infix, push operands in a stack. If the input is an operator, you pop operands, and concatenate operands and operator as a postfix, and save it back to the stack. Another method is using recursion. Since the first term in infix is always operator, you remove it and save it as op. Call the recursive method twice to get two operands. Declare a list to save two operands and op in sequence in the list. The return from all recursions (call stacks) is the final postfix expression.





