To find number of possible combinations of valid parentheses, we have to know Catalan number. Catalan numbers are a sequence of natural numbers that follow the formula showing below.
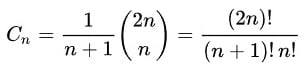
The first few Catalan numbers for n = 0, 1, 2, 3, 4, 5 … Cn = 1, 1, 2, 5, 14, 42, … Number of valid parentheses are one of example of Catalan numbers. When n=2, there are 2 possible expressions, (()), ()(). When n = 3, there are 5 possible expressions ((())), ()(()), ()()(), (())(), (()()). For any given n, there are Cn (Catalan number) of valid parentheses.
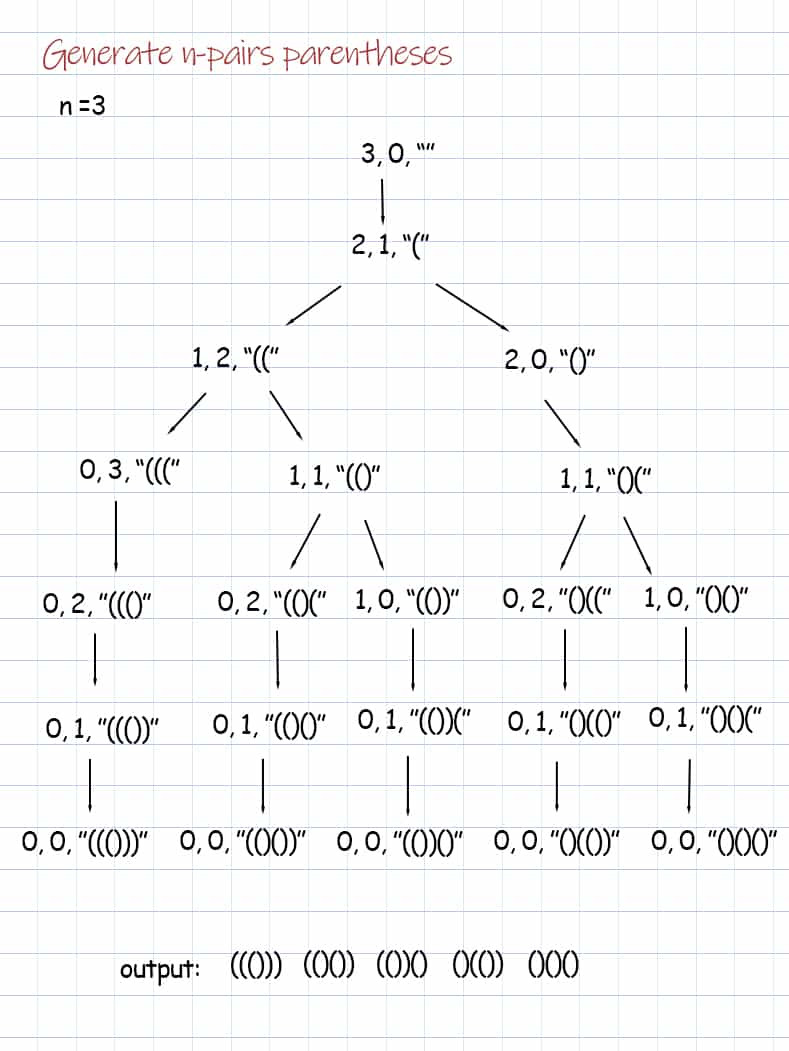
Given n, we can generate Cn valid expressions with n pairs parentheses. To print out all possible Cn expressions, we use backtracking. We define two variables as arguments of the recursive method. The variable open starts with input n. The close starts with 0. When adding a ‘(‘, the open decrease by 1 and the close increase by 1. When adding ‘)’, the close decreases by 1. When both open and close are 0, we have all possible valid combinations of parentheses. The time complexity is Catalan number Cn. n is input number.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | public class GenerateValidParentheses { //Wrapper, Time O(Cn), Space O(Cn), n in input number //Cn is Catalan number, Cn = (2n)!/(n+1)!n! public static void genValidParen(int n) { generate(n, 0, ""); } //DFS helper, Time O(n*Cn), Space O(Cn), extra loop to print private static void generate(int open, int close, String output) { if (open == 0 && close == 0) { System.out.println(output); return; } if (open > 0) generate(open-1, close+1, output + "("); if (close > 0) generate(open, close-1, output + ")"); } public static void main(String[] args) { int n = 3; System.out.println("All possible of "+ n +" pairs valid parentheses: "); genValidParen(n); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | //Recursion Wrapper, Time O(Cn), Space O(Cn), n in input number function genValidParen(n) { helper(n, 0, "", 0); } //Recursion helper, Time O(n*Cn), Space O(Cn), extra loop to print function helper(open, close, output, level) { console.log(level); if (open == 0 && close == 0) { console.log(output); return; } if (open > 0) helper(open-1, close+1, output + "(", level+1); if (close > 0) helper(open, close-1, output + ")", level+1); } let n = 3; console.log("All possible of "+ n +" pairs valid parentheses: "); genValidParen(n); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | #Recursion Wrapper, Time O(Cn), Space O(Cn), n in input number def genValidParen(n) : helper(n, 0, "") # Recursion helper, Time O(n*Cn), Space O(Cn), extra loop to print def helper(open, close, output) : if (open == 0 and close == 0) : print(output) return if open > 0: helper(open-1, close+1, output + "(") if close > 0: helper(open, close-1, output + ")") n = 3 print("All possible of "+ str(n) +" pairs valid parentheses: ") genValidParen(n); |
Doodle
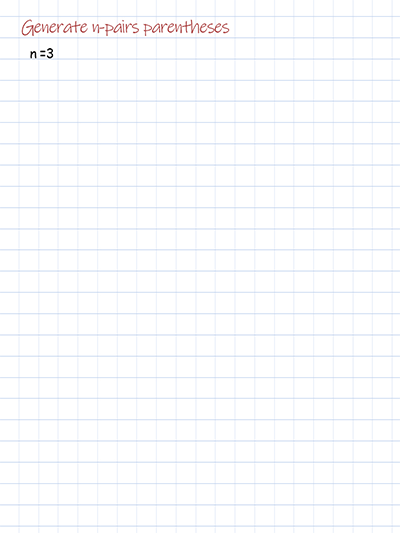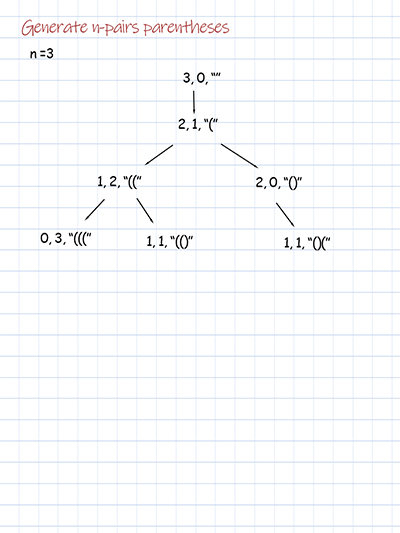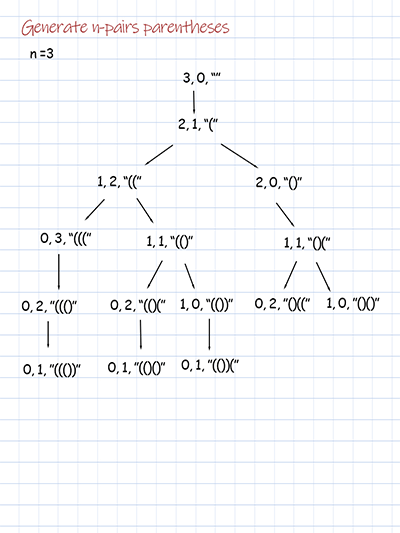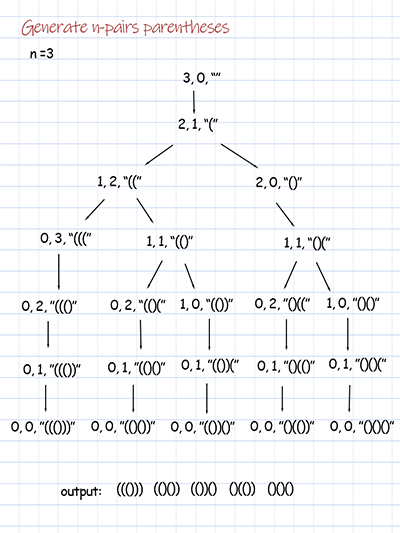
Output:
All possible of 3 pairs valid parentheses:
((()))
(()())
(())()
()(())
()()()
O Notation:
Time complexity:O(Cn), Cn is Catalan number, n is input number
Space complexity: Space O(Cn)
The time complexity is O(Cn). Cn is Catalan number.





