An Euler path is a trail in a graph that visits every edge exactly once. Here we use graph data structure to simulate the set of linked porker cards and find the Euler path between them. In a porker game, if two poker cards have matched suites and figures, they can be link together. Given set of porker cards, we are going to link matched card as an Euler path and find the longest possible one. Each card can be seen as a node in a graph. The matched two cards have a bi-directional edge between them. So the graph is undirected. This post is to find Euler path with Hierholzer’s algorithm.
How Hierholzer’s algorithm works?
- Find a closed tour in a graph.
start from any vertex v and follow a trail of edges until returning to v. The tour formed a closed tour.
- Find branches
If there is a vertex u that belongs to the current tour, but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u.
- Use backtrack to use all edges
keep following unused edges and removing them when we get stuck. When stuck, backtrack to the nearest vertex in the current path that has unused edges. Repeat the process until all the edges have been used.
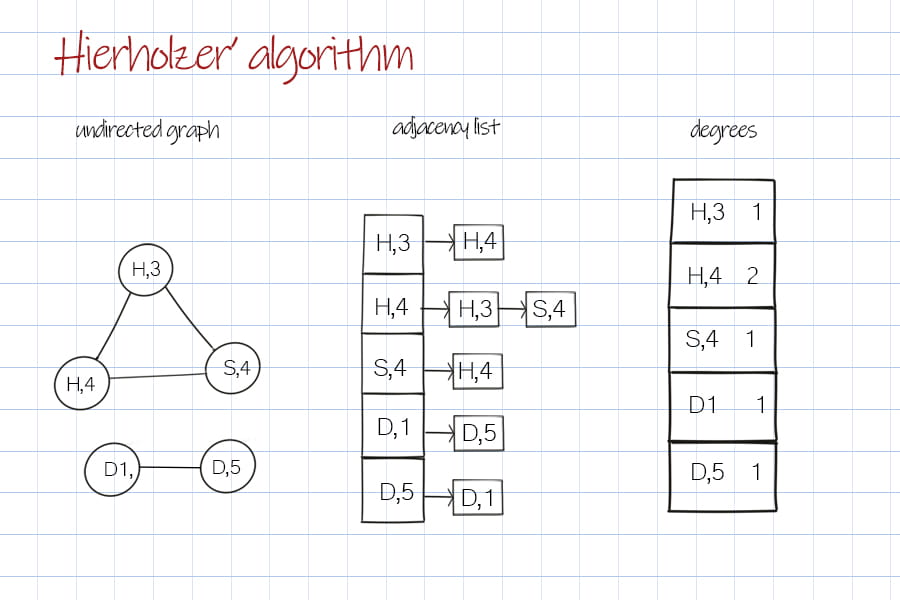
The set of cards will be the input to build an undirected graph as adjacency list. After building the graph, we start from the first key in adjacency list. The node’s degree is used to keep track the unvisited edges. A stack is to track the cards that have been visited. When the edge is visited, its degree will be decreased by 1. When the degree is 0, it is time to backtrack the card that is last visited and has unused edges. So that we bridge other links of the matched cards. Meanwhile the visited card popped from the stack will be saved in a doubly linked list, which link all possible matched cards. This double linked list is the result of one pass of Hierholzer run. It’s time complexity is O(E). E is the number of edges.
After we have solution to find Euler path with Hierholzer’s algorithm for undirected graph, we are asked to find the longest path from the first card. This is the extension of the problem. The answer is to add another layer of loop to have multiple Hierholzer runs. We iterate through all keys (all cards) in the adjacency list as the start node to run Hierholzer’s . The result is saved in a map. The key is the length of the matched cards in each Hierholzer run. The value is a linked list which maintains the linked matched cards with the same length. The map is sorted by key in descending order. The first key is the max number of the matched cards.
Amazon Interview Question:
As we all know that poker cards have four suites: Spades, Hearts, Clubs and Diamonds with figures from 1 to 13.Now you are given a set of poker cards, you can pick any one card as the first card. And except for the first card, you can only pick the card that has the same suit or figure with the previous one.Return the max number of cards you can.
For example: [(H, 3), (H, 4), (S, 4), (D, 5), (D, 1)], it returns 3 as follows: (H,3)–>(H,4)–>(S,4)
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 | import java.util.*; public class LongestPathMatchedCardsHierholzer { static class Card { String suite; String figure; //Constructor, Time O(1) Space O(1) Card (String s, String f) { suite = s; figure = f; } //either suite or figure are the same to match //Time O(1), Space O(1) public boolean matched(Object o) { if (o instanceof Card) { Card s = (Card) o; return this.suite == s.suite || this.figure == s.figure; } else { return false; } } //Time O(1), Space O(1) @Override public String toString() { return "("+ suite+", "+ figure +")"; } } //Use Hierholzer's algorithms, Time O(V*E), Space O(E+V) //E number is of edges, V is number of vertices public static int longestChains(List<Card> input) { Map<Card, LinkedList<Card>> adj = buildGraph(input); Map<Card,Integer> degrees = new LinkedHashMap<>(); for (Card key: adj.keySet()) { //number of degrees are the number of out edges degrees.put(key,adj.get(key).size()); } TreeMap<Integer, List<Set<Card>>> links = new TreeMap<>(Collections.reverseOrder()); //track all linked chains, keys are theirs sizes List<Card> allKeys = new ArrayList<>(adj.keySet()); //all nodes will be checked as start node for (int i = 0 ;i < allKeys.size(); i++) { Stack<Card> stack = new Stack<>(); //keep track visited nodes Set<Card> chain = new LinkedHashSet<>(); //keep track the linked cards(not necessary in order) Card first = allKeys.get(i); //choose one in adjacency list keys stack.push(first); //start node Card curr = first; while (!stack.empty()) { //run out cards if (degrees.get(curr) > 0) { //pick next unvisited edge stack.push(curr); //push to stack Card next = adj.get(curr).getLast(); degrees.put(curr, degrees.get(curr) - 1); //degree decrease adj.get(curr).removeLast(); curr = next;; //next one to visit } else { //backtracking when next is not linkable chain.add(curr); //add to chain curr = stack.peek(); //next to visit stack.pop(); } } int len = chain.size(); //save the chain size and chains in links, size is the key links.putIfAbsent(len, new LinkedList<>()); links.get(len).add(chain); } return links.firstKey(); //return the largest one } //Build undirected graph adjacency list from input, Time O(V^2), Space O(E+V) private static Map<Card, LinkedList<Card>> buildGraph(List<Card> input) { Map<Card, LinkedList<Card>> adj = new LinkedHashMap<>(); int n = input.size(); for (int i = 0; i < n-1; i++) { Card card1 = input.get(i); //get one node adj.putIfAbsent(card1, new LinkedList<>()); //save node to adjacency list for (int j = i+1; j < n; j++) { Card card2 = input.get(j); //get another node adj.putIfAbsent(card2, new LinkedList<>()); //save node to adjacency list if (card1.matched(card2)) { adj.get(card1).add(card2); //add edges adj.get(card2).add(card1); //add edges } } } return adj; } public static void main(String[] args) { //case1 String[][] input = {{"H","3"},{"H","4"},{"S","4"},{"D","1"}, {"D", "5"}}; //create nodes List<Card> nodes = new ArrayList<>(); int n = input.length; for (int i = 0; i < n; i++) { nodes.add(new Card( input[i][0], input[i][1])); } System.out.println("Case1 max number of cards: "+ longestChains(nodes)); //case2 String[][] input1 = {{"H","3"},{"H","4"},{"S","4"},{"D","1"}, {"D", "5"}, {"H", "1"}}; List<Card> nodes1 = new ArrayList<>(); int n1 = input1.length; for (int i = 0; i < n1; i++) { nodes1.add(new Card( input1[i][0], input1[i][1])); } System.out.println("Case2 max number of cards: "+ longestChains(nodes1)); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 | class Card { //Constructor, Time O(1) Space O(1) constructor (s, f) { this.suite = s; this.figure = f; } //either suite or figure are the same, Time O(1), Space O(1) matched(s) { return this.suite == s.suite || this.figure == s.figure; } //Time O(1), Space O(1) toString() { return "("+ this.suite+", "+ this.figure +")"; } } class LinkedCards { //Use Hierholzer's algorithms, Time O(V*E), Space O(E+V) //E number is of edges, V is number of vertices longestChains(input) { var adj = this.buildGraph(input); var degrees = new Map(); for (let entry of adj.entries()) { //number of degrees are the number of out edges degrees.set(entry[0],entry[1].length); } var links = new Map(); //track all chains, keys are theirs sizes var allKeys = [ ...adj.keys() ]; //all nodes will be checked as start node for (let i = 0; i < allKeys.length; i++) { let stack = []; //keep track visited nodes let chain = new Set(); //keep track the linked cards(not necessary in order) let first = allKeys[i]; //choose one in adjacency list keys stack.push(first); //start node let curr = first; while (stack.length != 0) { //run out cards if (degrees.get(curr) > 0) { //pick next unvisited edge stack.push(curr); //push to stack let list = adj.get(curr); let next = list[list.length-1]; degrees.set(curr, degrees.get(curr) - 1); //degree decrease adj.get(curr).pop(); curr = next; } else { //backtracking when next is not linkable chain.add(curr); //add to chain curr = stack[stack.length-1]; // peek stack.pop(); } } let len = chain.size; //save the chain size and chains in links, size is the key if (links.get(len) == null) links.set(len, new Array()); links.get(len).push(chain); } var linkskeys = [ ...links.keys() ]; linkskeys.sort( function ( a, b ) { return b - a; } ); // Sort the keys in descending order return linkskeys[0]; //return the largest one } //Build undirected graph adjacency list from input, Time O(V^2), Space O(E+V) buildGraph(input) { var adj = new Map(); var n = input.length; for (let i = 0; i < n-1; i++) { let card1 = input[i]; //get one node if (adj.get(card1) == null) //save node to adjacency list adj.set(card1, new Array()); for (let j = i+1; j < n; j++) { let card2 = input[j]; //get another node if (adj.get(card2) == null) //save node to adjacency list adj.set(card2, new Array()); if (card1.matched(card2)) { adj.get(card1).push(card2); //add edges adj.get(card2).push(card1); //add edges } } } return adj; } } var g = new LinkedCards(); //case1 var input = [["H","3"],["H","4"], ["S","4"],["D","1"], ["D", "5"]]; //create nodes var nodes = new Array(); var n = input.length; for (let i = 0; i < n; i++) { nodes.push(new Card( input[i][0], input[i][1])); } console.log("Case1 max number of cards: " + g.longestChains(nodes)); //case2 var input1 = [["H","3"],["H","4"], ["S","4"],["D","1"], ["D", "5"],["H", "1"]]; var nodes1 = new Array(); var n1 = input1.length; for (let i = 0; i < n1; i++) { nodes1.push(new Card( input1[i][0], input1[i][1])); } console.log("Case2 max number of cards: " + g.longestChains(nodes1)); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | class Card : #Constructor, Time O(1) Space O(1) def __init__(self,s, f) : self.suite = s self.figure = f #either suite or figure are the same, Time O(1), Space O(1) def matched(self, s) : return self.suite == s.suite or self.figure == s.figure #Time O(1), Space O(1) def __str__(self): return "(" + self.suite + ", "+ self.figure + ")" class LinkedCards : #Use Hierholzer's algorithms, Time O(V*E), Space O(E+V) #E number is of edges, V is number of vertices def longestChains(self, input): adj = self.createGraph(input) degrees = {}; #number of degrees are the number of out edges for k, v in adj.items(): degrees[k] = len(v) links = {} # track all linked chains, keys are theirs sizes allKeys = list(adj.keys()) #all nodes will be checked as start node for i in range(0, len(allKeys)): stack = [] #keep track visited nodes chain = set() #keep track the linked cards (not necessary in order) first = allKeys[i] #chose one in adjacency list keys stack.append(first) #start node curr = first while len(stack) != 0: #finish cards if degrees.get(curr) > 0 : stack.append(curr) #pick next unvisited edge next = adj.get(curr)[-1] degrees[curr]= degrees.get(curr) - 1 # degree decrease adj.get(curr).pop() curr = next else: #backtracking when next is not linkable chain.add(curr) #add to chain curr = stack[-1] # peek stack.pop() size = len(chain) #save the chain size and chains in links, size is the key if size not in links: links[size] = [] links[size].append(chain) linkskeys = list (links.keys()) sorted(linkskeys, reverse = True) #sort the key in descending order return linkskeys[0] #return the largest one #Build undirected graph adjacency list from input, Time O(V^2), Space O(E+V) def createGraph(self, input) : adj = {} n = len(input) for i in range(0, n-1): card1 = input[i] #get one node if card1 not in adj: #save node to adjacency list adj[card1] = [] for j in range(i+1, n): card2 = input[j]; #get another node if card2 not in adj: # save node to adjacency list adj[card2] = [] if card1.matched(card2) : adj[card1].append(card2) #add edges adj[card2].append(card1) #add edges return adj g = LinkedCards() #case1 input = [["H","3"], ["H","4"], ["S","4"], ["D","1"], ["D", "5"]] #create nodes n = len(input) nodes = [None]*(n) for i in range(0, n) : nodes[i] = Card(input[i][0], input[i][1]) print("Case1 max number of cards: " + str(g.longestChains(nodes))) #case2 input1 = [["H","3"], ["H","4"], ["S","4"], ["D","1"], ["D", "5"],["H", "1"]] n1 = len(input1) nodes1 = [None]*(n1) for i in range(0, n1) : nodes1[i] = Card(input1[i][0], input1[i][1]) print("Case2 max number of cards: " + str(g.longestChains(nodes1))) |
Output:
(H, 3), (H, 4), (S, 4), (D, 1), (D, 5)
Max number of cards: 3
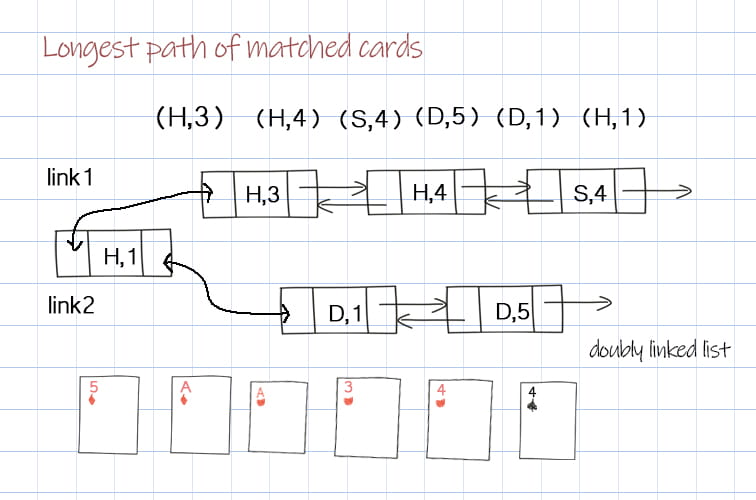
Links: (H, 3), (H, 4), (S, 4), (D, 1), (D, 5), (H, 1)
Max number of cards: 6
Please note the test case2. Sometimes when a new card is added, it makes two linked lists merge as one. For example, we have the first linked list of (H,3), (H,4), (S,4), and the second linked list (D,1), (D5). When adding new card (H,1), it connect two linked lists to be one (D,5), (D,1), (H,1), (H,3), (H,4), (S,4).
O Notation:
Time complexity: O(E*V)
Space complexity: O(E+V)
V is total number of cards, E is number of matched cards
Download LongestPathOfMatchedCards.java
Download LongestPathOfMatchedCards.js
Download LongestPathOfMatchedCards.py





