A graph is a data structure that consists of a set of nodes (vertices) connected by edges. A graph is cyclic if the graph comprises a path that starts from a node and ends at the same node. In this post, a simplified solution is provided to detect cycle and remove cycle in directed graph.
To detect cycle in a directed graph, we use backtracking technique in depth first search. We define a variable backtrack to keep track this. The initial value is false for each node. When using depth first search to visit each node, the value of backtrack for the visited node is set to be true. Next is to visit this node’s neighbors. If there is cycle, the same node will be visited again and dfs helper recursive method returns true without backtracking. If there is no cycle, the call stack will return and the backtrack value will be reset to false. When the backtrack is false and the node is already visited, dfs helper method will return false and no cycle is detected.
![]()
After a cycle is detected, next is to remove cycles in graph. However it is a complicated problem. You can refer the reduction of Directed Cyclic Graph for details. The problem cannot be solved in an hour interview. But if you assume there is only one cycle, you can apply a simple brute force solution. That is to remove one edge at a time and call detect cycle to check whether the cycle is gone. The following is the source code to
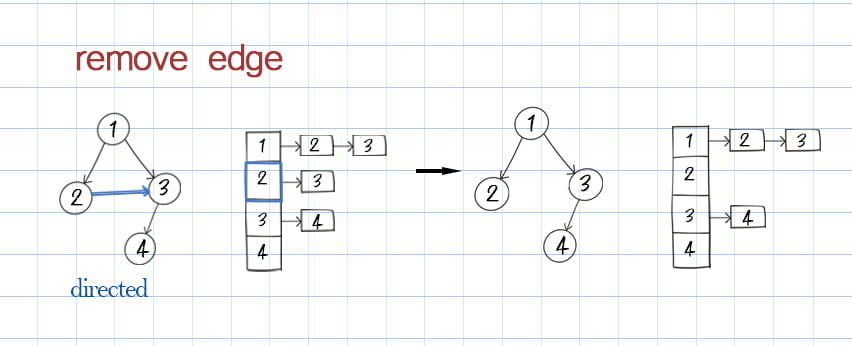
Facebook Interview Question:
class DirectedGraphNode {
int label;
List
DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<>();
}
}
check if there is a cycle in a directed graph, if there is a cycle, remove the cycle.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 | import java.util.*; import java.util.concurrent.CopyOnWriteArrayList; public class GraphDetectCycleAndRemove { static class DirectedGraphNode { int label; List<DirectedGraphNode> neighbors ; //constructor, Time O(1), Space O(1) DirectedGraphNode(int x) { label = x; neighbors = new CopyOnWriteArrayList<>(); } public String toString() { return String.valueOf(label); } } //adjacency list Map<Integer, DirectedGraphNode> adj = new HashMap<>(); //Add nodes and edges, Time O(1), Space O(1) public void addEdge(int a, int b) { adj.putIfAbsent(a, new DirectedGraphNode(a)); adj.putIfAbsent(b, new DirectedGraphNode(b)); DirectedGraphNode node1 = adj.get(a); DirectedGraphNode node2 = adj.get(b); node1.neighbors.add(node2); //add edge } //Detect whether there is cycle in graph, DFS, Time O(V+E), Space O(V) public boolean detectCycle() { Map<Integer, Boolean> visited = new HashMap<>(); Map<Integer, Boolean> backTrack = new HashMap<>(); for (int key: adj.keySet()) { visited.put(key, false); backTrack.put(key, false); } for (Integer key: adj.keySet()) { if (!visited.get(key)) { if (cycleUtil(key, visited, backTrack)) { return true; } } } return false; } //DFS helper, Recursion + memoization, Time O(V+E), Space O(V) private boolean cycleUtil(int v, Map<Integer, Boolean> visited, Map<Integer, Boolean> backTrack){ if (backTrack.get(v)) return true; if (visited.get(v)) return false; visited.put(v, true); backTrack.put(v, true);; for (DirectedGraphNode ne : adj.get(v).neighbors) { if (cycleUtil(ne.label, visited, backTrack)) return true; } backTrack.put(v, false); return false; } //Check all edges, remove one edge at a time and check whether the cycle is removed //Time O(E*(V+E)), Space O(V) public boolean removeCycle() { for (int key: adj.keySet()) { for (DirectedGraphNode ne: adj.get(key).neighbors) { removeEdge(key, ne.label); boolean b = detectCycle(); if (!b) {//no more cycle System.out.println("remove edge: "+ key+","+ne); return true; } else addEdge(key, ne.label); //add back } } return false; } //Remove edges, Time O(1), Space O(1) public void removeEdge(int a, int b) { DirectedGraphNode node1 = adj.get(a); DirectedGraphNode node2 = adj.get(b); if (node1 == null || node2 == null) return; node1.neighbors.remove(node2); } public static void main(String a[]) { //build directed graph with one cycle /* * 1 * > | * / V * 0 <- 2 * | * V * 3 */ GraphDetectCycleAndRemove g = new GraphDetectCycleAndRemove(); g.addEdge(0, 1); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); boolean hasCycle = g.detectCycle(); System.out.println("has cycle: " + hasCycle); if (hasCycle) g.removeCycle(); hasCycle = g.detectCycle(); System.out.println("has cycle: " + hasCycle); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 | class DirectedGraphNode { //constructor, Time O(1), Space O(1) constructor(x) { this.label = x; this.neighbors = new Array(); } } class GraphDetectCycleAndRemove { //constructor, Time O(1), Space O(1) constructor(x) { this.adj = new Map(); } //Add nodes and edges, Time O(1), Space O(1) addEdge(a, b) { if (this.adj.get(a) == null) this.adj.set(a, new DirectedGraphNode(a)); if (this.adj.get(b) == null) this.adj.set(b, new DirectedGraphNode(b)); var node1 = this.adj.get(a); var node2 = this.adj.get(b); node1.neighbors.push(node2); //add edge } //Detect whether there is cycle in graph, DFS, Time O(V+E), Space O(V) detectCycle() { var visited = new Map(); var backTrack = new Map(); for (let entry of this.adj.entries()) { visited.set(entry[0], false); backTrack.set(entry[0], false); } for (let entry of this.adj.entries()) { if (!visited.get(entry[0])) { if (this.cycleUtil(entry[0], visited, backTrack)) { return true; } } } return false; } //DFS helper, Recursion + memoization, Time O(V+E), Space O(V) cycleUtil(v, visited, backTrack){ if (backTrack.get(v)) return true; if (visited.get(v)) return false; visited.set(v, true); backTrack.set(v, true);; for (let ne of this.adj.get(v).neighbors) { if (this.cycleUtil(ne.label, visited, backTrack)) return true; } backTrack.set(v, false); return false; } //Check all edges, remove one edge at a time and check whether the cycle is removed //Time O(E*(V+E)), Space O(V) removeCycle() { for (let entry of this.adj.entries()) { for (let ne of this.adj.get(entry[0]).neighbors) { this.removeEdge(entry[0], ne.label); let b = this.detectCycle(); if (!b) {//no more cycle console.log("remove edge: " + entry[0] + "," + ne.label); return true; } else this.addEdge(entry[0], ne.label); //add back } } return false; } //Remove edges, Time O(1), Space O(1) removeEdge(a, b) { var node1 = this.adj.get(a); var node2 = this.adj.get(b); if (node1 == null || node2 == null) return; var ne =node1.neighbors; var index = ne.indexOf(node2); if(index >= 0) ne.splice(index, 1); } } //build directed graph with one cycle /* 1 > | / V 0 <- 2 | V 3 */ var g = new GraphDetectCycleAndRemove(); g.addEdge(0, 1); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); let hasCycle = g.detectCycle(); console.log("has cycle: " + hasCycle); if (hasCycle) g.removeCycle(); hasCycle = g.detectCycle(); console.log("has cycle: " + hasCycle); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 | class DirectedGraphNode : #constructor, Time O(1), Space O(1) def __init__(self, x): self.label = x self.neighbors = [] class GraphDetectCycleAndRemove : #constructor, Time O(1), Space O(1) def __init__(self) : self.adj = {} #Add nodes and edges, Time O(1), Space O(1) def addEdge(self, a, b): if a not in self.adj: self.adj[a] = DirectedGraphNode(a) if b not in self.adj: self.adj[b] = DirectedGraphNode(b) node1 = self.adj[a] node2 = self.adj[b] node1.neighbors.append(node2); #add edge # Detect whether there is cycle in graph, DFS, Time O(V+E), Space O(V) def detectCycle(self) : visited = {} backTrack = {} for k, v in self.adj.items(): visited[k] = False backTrack[k] = False for k, v in self.adj.items() : if visited[k] == False: if (self.cycleUtil(k, visited, backTrack)) : return True return False # DFS helper, Recursion + memoization, Time O(V+E), Space O(V) def cycleUtil(self, v, visited, backTrack): if backTrack[v]: return True if visited[v]: return False visited[v] = True backTrack[v] = True for ne in self.adj[v].neighbors : if self.cycleUtil(ne.label, visited, backTrack): return True backTrack[v] = False return False #Check all edges, remove one edge at a time and re-check whether the cycle is removed #Time O(E*(V+E)), Space O(V) def removeCycle(self) : for k, v in self.adj.items(): for ne in self.adj[k].neighbors : self.removeEdge(k, ne.label) b = self.detectCycle() if (b == False) : #no more cycle print("remove edge: " + str(k) + "," + str(ne.label)) return True else: self.addEdge(k, ne.label); #add back return False #Remove edges, Time O(1), Space O(1) def removeEdge(self, a, b) : node1 = self.adj[a] node2 = self.adj[b] if node1 == None or node2 == None: return node1.neighbors.remove(node2) # build directed graph with one cycle # /* # 1 # > | # / V # 0 <- 2 # | # V # 3 # g = GraphDetectCycleAndRemove() g.addEdge(0, 1) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) hasCycle = g.detectCycle() print("has cycle: " + str(hasCycle)) if hasCycle: g.removeCycle() hasCycle = g.detectCycle() print("has cycle: " + str(hasCycle)) |
Output:
has cycle: true
remove edge: 0,1
has cycle: false
O Notation:
Time complexity: O(E*(V+E))
Space complexity: O(V)
V is number of vertices, E is number of edges.
Download GraphDetectCycleAndRemove.java
Download GraphDetectCycleAndRemove.js
Download GraphDetectCycleAndRemove.py





